【高校物理の要点】熱サイクル～熱機関と熱効率～

本記事では、『熱サイクル～熱機関と熱効率～』について解説していきたいと思います。

熱機関

蒸気機関のように，熱の吸収，放出をくり返して熱を仕事に変換する装置を熱機関という。

気体の状態が，ある状態AからA→B→C→D→Aのようにさまざまな状態変化を経てもとの状態Aにもどるとき，これをサイクルという。

＜熱サイクルの例＞
下図のような熱サイクルを考えよう。ここでは単原子分子理想気体\(n\)[mol]に対して，図の4つの過程を繰り返して状態を変化させた。

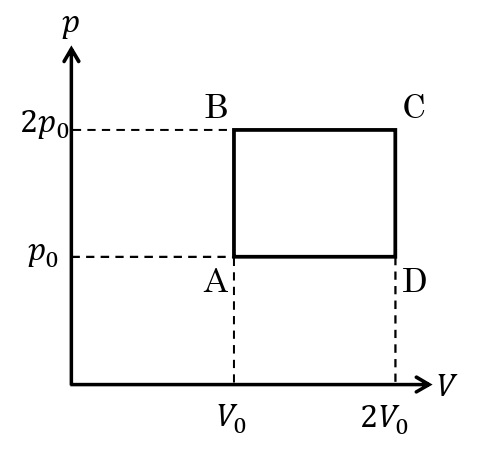
まず，ボイルシャルルの法則より，

\begin{eqnarray}\frac{p_0V_0}{T_A}=\frac{2p_0V_0}{T_B}=\frac{2p_0\cdot 2V_0}{T_C}=\frac{p_0\cdot 2V_0}{T_D}\end{eqnarray}

よって，\(T_B=2T_A\)，\(T_C=4T_A\)，\(T_D=2T_A\)が成り立つ。

A→Bの過程（定積加圧）

定積変化より，

\begin{eqnarray}W_{AB}=0\end{eqnarray}

また，

\begin{eqnarray}\displaystyle\it\Delta U_{AB}\rm=\frac{3}{2}\it nR\rm(\it T_B\rm-\it T_A\rm)=\frac{3}{2}\it nRT_A\end{eqnarray}

よって，熱力学第一法則より，

\begin{eqnarray}Q_{AB}=\it\Delta U_{AB}\rm+\it W_{AB}\rm=\dfrac{3}{2}\it nRT_A\end{eqnarray}

B→Cの過程（定圧膨張）

定圧変化より，

\begin{eqnarray}W_{BC}&=&2p_0(2V_0-V_0)\\&=&2p_0V_0\\&=&2nRT_A\end{eqnarray}

また，

\begin{eqnarray}\displaystyle\it\Delta U_{BC}&=&\frac{3}{2}\it nR\rm(\it T_C-T_B\rm)\\&=&\frac{3}{2}\it nR\cdot\rm2\it T_A\\&=&3\it nRT\end{eqnarray}

よって，熱力学第一法則より，

\begin{eqnarray}Q_{BC}=\it\Delta U_{BC}\rm+\it W_{BC}=\rm5\it nRT_A\end{eqnarray}

C→Dの過程（定積減圧）

定積変化より，\begin{eqnarray}W_{CD}=0\end{eqnarray}

また，

\begin{eqnarray}\displaystyle\it\Delta U_{CD}\rm&=&\frac{3}{2}\it nR\rm(\it T_D-T_C\rm)\\&=&-3\it nRT_A\end{eqnarray}

よって，熱力学第一法則より，\begin{eqnarray}Q_{CD}=\it\Delta U_{CD}\rm+\it W_{CD}\rm=-3\it nRT_A\end{eqnarray}

D→Aの過程（定圧圧縮）

定圧変化より，\begin{eqnarray}W_{DA}&=&p_0(V_0-2V_0)\\&=&-p_0V_0\\&=&-nRT_A\end{eqnarray}

また，

\begin{eqnarray}\displaystyle\it\Delta U_{DA}\rm&=&\frac{3}{2}\it nR\rm(\it T_A-T_D\rm)\\&=&-\frac{3}{2}\it nRT_A\end{eqnarray}

よって，熱力学第一法則より，\begin{eqnarray}Q_{DA}=\it\Delta U_{DA}\rm+\it W_{DA}\rm=-\dfrac{5}{2}\it nRT_A\end{eqnarray}

結果

ここで，1サイクルで気体が吸収する熱量\(Q_{in}\)[J]と，放出する熱量\(Q_{out}\)[J]とすると，

\begin{eqnarray}Q_{in}&=&Q_{AB}+Q_{BC}\\&=&\frac{3}{2}nRT_A+5nRT_A\\&=&\frac{13}{2}nRT_A\end{eqnarray}

\begin{eqnarray}Q_{out}&=&Q_{CD}+Q_{DA}\\&=&3nRT_A+\frac{5}{2}nRT_A\\&=&\frac{11}{2}nRT_A\end{eqnarray}

となる。また，1サイクルのうち，B→Cの過程で気体は外部に対し\(W_{BC}=2nRT_A\)の仕事をし，D→Aの過程で気体は外部から\(|W_{DA}|=nRT_A\)の仕事をされる。したがって，この1サイクルで気体がする仕事は，

\begin{eqnarray}W&=&2nRT_A-nRT_A\\&=&nRT_A\\&=&p_0V_0\\&=&(2p_0-p_0)(2V_0-V_0)\end{eqnarray}

と変形できる。これは，1サイクルが\(p\)-\(V\)グラフで囲む領域の面積に等しい。

熱効率

1サイクルの中で高温の物体から吸収した熱量を\(Q_{in}\)[J]，低温の物体に放出した熱量を\(Q_{out}\)[J]とする。1サイクルするともとの状態にもどるので内部エネルギーの変化\(\it\Delta U\)は\(0\)となる。よって，熱力学第一法則より，

\begin{eqnarray}W=Q_{in}-Q_{out}\end{eqnarray}

が成り立つ。1サイクルで，吸収した熱量\(Q_{in}\)のうち，仕事\(W\)に変換された割合を熱効率という。以上より，熱効率は

\begin{eqnarray}e=\frac{W}{Q_{in}}=1-\frac{Q_{out}}{Q_{in}}\end{eqnarray}

とあらわすことができる。

＜例＞で扱った熱サイクルの熱効率を求めてみよう。ここで，1サイクルで吸収した熱量は\(Q_{in}=\dfrac{13}{2}nRT_A\)，\(W=nRT_A\)であることから

\begin{eqnarray}e=\frac{W}{Q_{in}}=\frac{nRT_A}{\frac{13}{2}nRT_A}=\frac{2}{13}\end{eqnarray}

となる。