【高校物理の要点】速度と加速度～位置、速度、加速度・相対速度・等加速度直線運動～

2024年3月8日2024年7月27日

このサイトはアフィリエイト広告（Amazonアソシエイト含む）を掲載しています。

本記事では、『速度と加速度～位置、速度、加速度・相対速度・等加速度直線運動～』について解説していきたいと思います。

筆者について

大学受験物理講師・ともくん

青森県出身。37歳。

経歴　東北大学物理学科→東北大学大学院理学研究科物理学専攻→公務員(教職ではない)→塾業界に転職。講師歴約10年(物理・数学)

歴代合格実績：旧帝大医学部、国公立大・私大医学部、東工大、旧帝大等多数

長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。

速度と加速度

位置と変位

位置：$\overrightarrow{r}=\overrightarrow{r}(t)$

変位：$\it\Delta \overrightarrow{r}=\overrightarrow{r}\rm(\it t\rm+\it\Delta t\rm)-\it\overrightarrow{r}\rm(\it t\rm)$

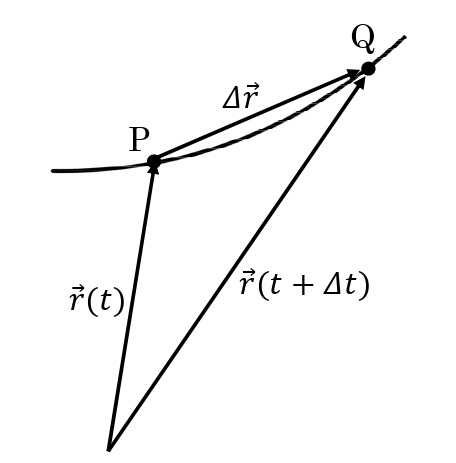
物体が運動するというのは，その位置ベクトル$\overrightarrow{r}$が時間とともに変化しているということである。つまり，$\overrightarrow{r}$は時刻$t$の関数$\overrightarrow{r}=\overrightarrow{r}(t)$であらわすことができる。

物体が点Pから点Qまで移動したとする。点Oを基準とした点P，Qの位置ベクトルをそれぞれ$\overrightarrow{r}(t)$，$\overrightarrow{r}(t+\it\Delta \rm t)$を通過したとする。このとき，位置ベクトルの変化$\it\Delta \overrightarrow{r}=\overrightarrow{r}\rm(\it t\rm+\it\Delta t\rm)-\it\overrightarrow{r}\rm(\it t\rm)$を$\it\Delta t$の間の変位という。

速度

平均の速度\begin{eqnarray}\displaystyle\overrightarrow{\overline{v}}=\frac{\it\Delta\overrightarrow{r}}{\it\Delta t}=\frac{\overrightarrow{r}(t+\it\Delta t\rm)-\it\overrightarrow{r}\rm(\it t\rm)}{\it\Delta t}\end{eqnarray}

瞬間の速度
\begin{eqnarray}\displaystyle\overrightarrow{v}&=&\lim_{\it\Delta t \to \rm0}\frac{\it\Delta\overrightarrow{r}}{\it\Delta t}\\&=&\lim_{\it\Delta t \to \rm0}\frac{\overrightarrow{r}(t+\it\Delta t\rm)-\it\overrightarrow{r}\rm(\it t\rm)}{\it\Delta t}\\&=&\frac{d\overrightarrow{r}(t)}{dt}\end{eqnarray}

時間$\it\Delta t$の間に，物体が点P（位置ベクトル$\overrightarrow{r}(t)$）から点Q（位置ベクトル$\overrightarrow{r}(t+\it\Delta t\rm)$）に移動したとする。このとき，変位$\it\Delta \overrightarrow{r}$を経過時間$\it\Delta t$で割ったのもの$\displaystyle\overrightarrow{\overline{v}}=\frac{\it\Delta \overrightarrow{r}}{\it\Delta t}$を$\it\Delta t$の間の平均の速度という。

さらに，$\overrightarrow{\overline{v}}$の式において，経過時間$\it\Delta t$を0に近づけていくと，$\overrightarrow{\overline{v}}$はある一定の値$\overrightarrow{v}$に近づいていく。この$\overrightarrow{v}$を，時刻$t$における瞬間の速度(あるいは単に，速度)という。

相対速度

Aから見たBの相対速度：$\overrightarrow{v_{AB}}=\overrightarrow{v_B}-\overrightarrow{v_A}$

物体A，Bの速度をそれぞれ$\overrightarrow{v_A}$，$\overrightarrow{v_B}$とする。物体Aから見た物体Bの相対速度（Aに対するBの相対速度）を$\overrightarrow{v_{AB}}$とすると，$\overrightarrow{v_{AB}}=\overrightarrow{v_B}-\overrightarrow{v_A}$と表せる。

加速度

平均の加速度
\begin{eqnarray}\displaystyle\overrightarrow{\overline{a}}=\frac{\it\Delta \overrightarrow{v}}{\it\Delta t}=\frac{\overrightarrow{v}(t+\it\Delta t\rm)-\it\overrightarrow{v}\rm(\it t\rm)}{\it\Delta t}\end{eqnarray}

瞬間の加速度
\begin{eqnarray}\displaystyle\overrightarrow{a}&=&\lim_{\it\Delta t \to \rm0}\frac{\it\Delta\overrightarrow{v}}{\it\Delta t}\\&=&\lim_{\it\Delta t \to \rm0}\frac{\overrightarrow{v}(t+\it\Delta t\rm)-\it\overrightarrow{v}\rm(\it t\rm)}{\it\Delta t}\\&=&\frac{d\overrightarrow{v}\rm(\it t\rm)}{dt}\\&=&\it\frac{d^{\rm2}\it\overrightarrow{r}\rm(\it t\rm)}{\it dt^{\rm2}}\end{eqnarray}

物体が時刻$t$に点Pを$\overrightarrow{v}(t)$で通過し，時刻$t+\it\Delta t$に点Qを$\overrightarrow{v}(t+\it\Delta t\rm)$で通過したとする。このとき，速度の変化$\it\Delta \overrightarrow{v}$を経過時間$\it\Delta t$で割ったのもの$\displaystyle\overrightarrow{\overline{a}}=\frac{\it\Delta \overrightarrow{v}}{\it\Delta t}$を$\it\Delta t$の間の平均の加速度という。

さらに，$\overrightarrow{\overline{a}}$の式において，経過時間$\it\Delta t$を0に近づけていくと，$\overrightarrow{\overline{a}}$はある一定の値$\overrightarrow{a}$に近づいていく。この$\overrightarrow{a}$を，時刻$t$における瞬間の加速度(あるいは単に，加速度)という。

$v$-$t$グラフと変位，加速度

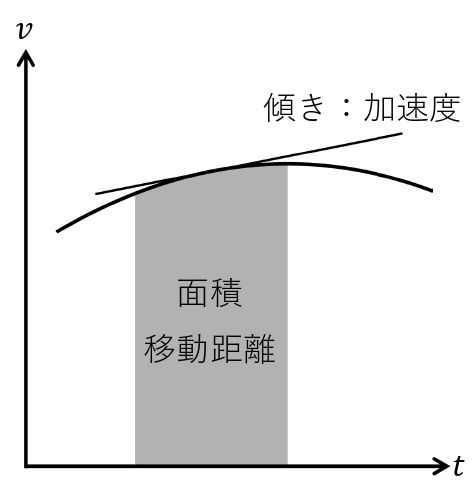
$x$軸に沿った物体の運動について，物体の速度$v$と時刻$t$との関係を表すグラフを，$v$-$t$グラフという。

$v$-$t$グラフの接線の傾きは，瞬間の加速度に等しい。
$v$-$t$グラフと$t$軸で固まれる部分の面積は，物体の移動距離に等しい。ただし，$v>0$の区間では変位は正，$v<0$の区間では変位は負である。

等速度運動

等速直線運動の式：$\it\Delta x=v_{\rm0}t$

速度が常に一定であるような運動を等速直線運動または等速度運動という。$x$軸に沿って，物体が速度$v_0$の等速度運動をする場合について，時間$t$だけ経過する間の物体の変位を$\it\Delta x$とすると$\it\Delta x=v_{\rm0}\it t$となる。

等加速度直線運動

等加速度直線運動の3公式
　①　$v=v_0+at$
　②　$\displaystyle\it\Delta x=v_{\rm0}t\rm+\frac{\rm1}{\rm2}\it at^{\rm2}$
　③　$v^2-v_0^2=2a\it\Delta x$

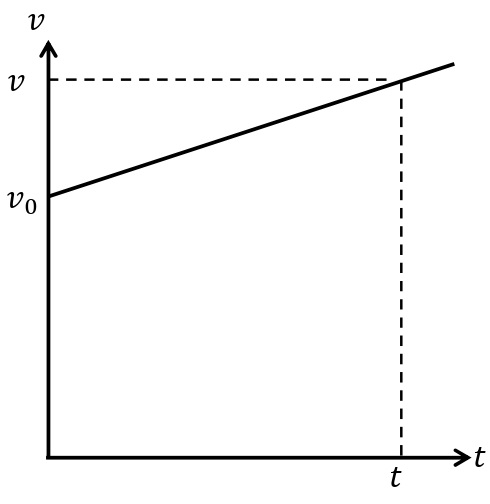
物体が直線上を一定の加速度で運動しているとき，この運動を等加速度直線運動という。物体が$x$軸に沿って，初速度$v_0$，加速度$a$の等加速度運動をする場合について考える。時刻$t=0$から時刻$t$までの物体の変位を$\it\Delta x$，時刻$t$の瞬間の物体の速度を$v$とする（下図）。

加速度$a$は直線の傾きであらわされるので，

\begin{eqnarray}a&=&\frac{v-v_0}{t}\\v&=&v_0+at\end{eqnarray}

が成り立つ。また，変位$\it\Delta x$は，図の台形の面積であらわされるので，

$$\displaystyle\it\Delta x=\rm\frac{1}{2}(\it v_{\rm0}\rm+\it v\rm)\it t$$

となる。ここで，$v=v_0+at$を代入すると，

$$\displaystyle\it\Delta x=\rm\frac{1}{2}(\rm2\it v_{\rm0}\rm+\it at\rm)\it t=v_{\rm0}\it t\rm+\rm\frac{1}{2}\it at^{\rm2}$$

が成り立つ。また，$v=v_0+at$より$\displaystyle t=\frac{v-v_0}{a}$とし，$\displaystyle\it\Delta x=v_{\rm0}\it t\rm+\frac{1}{2}\it at^{\rm2}$に代入すると，

\begin{eqnarray}\it\Delta x&=&v_{\rm0}\cdot\left(\it\frac{v-v_{\rm0}}{\it a}\right)\rm+\frac{1}{2}\it a\left(\frac{v-v_{\rm0}}{a}\right)^{\rm2}\\ &=&\frac{2\it v_{\rm0}\it v-\rm2\it v_{\rm0}^{\rm2}\rm+\it v^{\rm2}-\rm2\it v_{\rm0}\it v\rm+\it v_{\rm0}^{\rm2}}{2\it a}\\ &=&\frac{v^2-v_{\rm0}^2}{2a}\\ v^2-v_0^2&=&2a\it\Delta x \end{eqnarray}

が得られる。以上から，物体が直線上を一定の加速度$a$で運動しているとき，$v=v_0+at$，$\displaystyle\it\Delta x\rm=\it v_{\rm0}t\rm+\frac{\rm1}{\rm2}\it at^{\rm2}$，$v^2-v_0^2=2a\it\Delta x$の3公式が成り立つ。