本記事では、『慣性力～慣性力と遠心力～』について解説していきたいと思います。
大学受験物理講師・ともくん
青森県出身。37歳。
経歴 東北大学物理学科→東北大学大学院理学研究科物理学専攻→公務員(教職ではない)→塾業界に転職。講師歴約10年(物理・数学)
歴代合格実績：旧帝大医学部、国公立大・私大医学部、東工大、旧帝大等多数
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
慣性力
慣性力
地上に対して加速度\(\overrightarrow{a}\)で運動している観測者から見ると，質量\(m\)の物体は，慣性力\(-m\overrightarrow{a}\)を受けている。
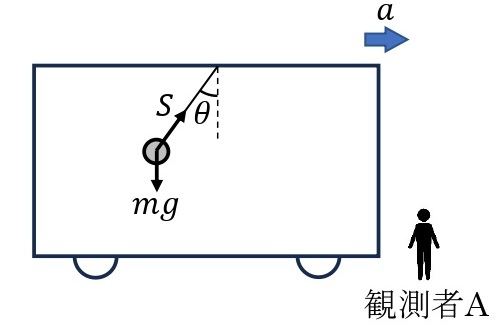
水平方向に加速度\(a\)[m/s²]で等加速度直線運動をする電車の中で，天井から軽いひもで質量\(m\)[kg]のおもりをつるした。地上に静止している観測者Aには，傾いて水平方向に等加速度直線運動しているように見える。よって，鉛直に対するひもの傾きを\(\theta\)，ひもの張力を\(S\)[N]とすると，以下の式が成り立つ。
水平方向の運動方程式：\(ma=S\sin\theta\)
鉛直方向の力のつりあい：\(S\cos\theta=mg\)
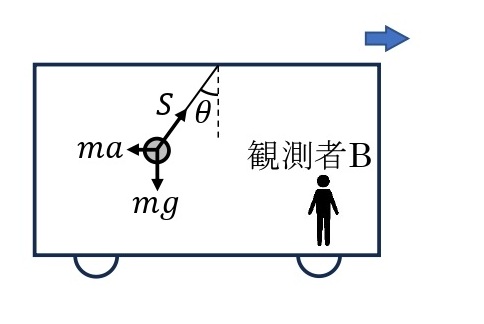
一方，電車の中の観測者Bには，静止しているように見えるので，慣性の法則は成りたたないようにみえる。しかし，糸の張力と重力以外に，電車の加速方向と逆向きに慣性力\(ma\)がはたらいていると考えると，以下の式が成り立ち，慣性の法則が成り立つとみなせる。
水平方向の力のつりあい：\(ma=S\sin\theta\)
鉛直方向の力のつりあい：\(S\cos\theta=mg\)
一般に，加速度運動をしている観測者が物体の運動を観測する場合，運動の法則は成りたたないようにみえるが実際にはたらく力のほかに慣性力をあわせて考えると，運動の法則が成りたつ。
加速度\(\overrightarrow{a}\)で運動する観測者が，力\(\overrightarrow{F}\)を受けて運動する質量\(m\)の物体を観測するとき，その加速度を\(\overrightarrow{a’}\)とする。このとき，実際にはたらく力\(\overrightarrow{F}\)のほかに慣性力\(-m\overrightarrow{a}\)を考えれば運動方程式は
$$m\overrightarrow{a’}=\overrightarrow{F}+(-m\overrightarrow{a})$$
のようになる。
遠心力
遠心力
半径\(r\)，速さ\(v=r\omega\)の等速円運動をしている質量\(m\)の物体は，この物体とともに円運動をする観測者から見ると，大きさ\(\displaystyle f=mr\omega^2=m\frac{v^2}{r}\)の遠心力がはたらく。
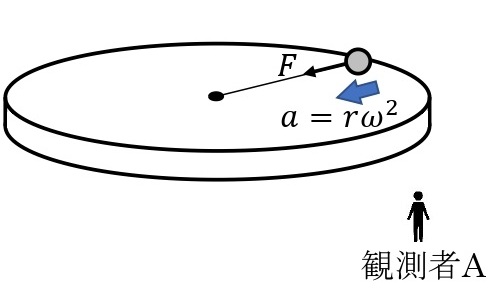
なめらかな回転板上での，糸の他端に質量\(m\)[kg]の小球をつなぎ，等速円運動させる。地上に静止している観測者Aから見ると，小球は糸の張力(大きさ\(F\)[N])を向心力として小球が等速円運動をしているように見える。よって，等速円運動の半径を\(r\)[m]，角速度を\(\omega\)[rad/s]，速さを\(v\)[m/s]とすると，
運動方程式：$$\displaystyle mr\omega^2=F または m\frac{v^2}{r}=F$$
が成りたつ。
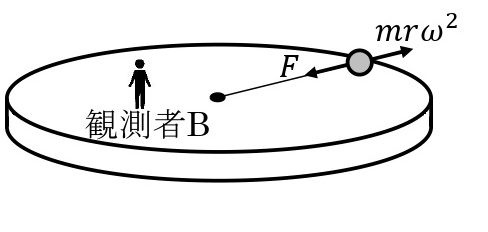
一方，小球とともに回転している観測者Bから見ると，小球が静止して見えるので，慣性の法則は成りたたないようにみえる。しかし，糸の張力の他に，それとつりあう外向きの遠心力\(\displaystyle \left(=mr\omega^2=m\frac{v^2}{r}\right)\)がはたらいていると考えると，以下の式が成り立ち，慣性の法則が成り立つとみなせる。
遠心力と張力のつりあい：$$\displaystyle mr\omega^2=F または m\frac{v^2}{r}=F$$
以上から，遠心力は，向心力の向き(等速円運動の加速度の向き)と逆向きで，その大きさ$f$[N]は
$$\displaystyle f=mr\omega^2 または f=m\frac{v^2}{r}$$
であらわすことがわかる。
コメント