本記事では、『単振動～単振動の変位・速度・加速度・ばね振り子・単振り子～』について解説していきたいと思います。
大学受験物理講師・ともくん
青森県出身。37歳。
経歴 東北大学物理学科→東北大学大学院理学研究科物理学専攻→公務員(教職ではない)→塾業界に転職。講師歴約10年(物理・数学)
歴代合格実績：旧帝大医学部、国公立大・私大医学部、東工大、旧帝大等多数
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
単振動
下図のように，等速円運動する物体に平行光線を当てたときの影の運動を単振動という。
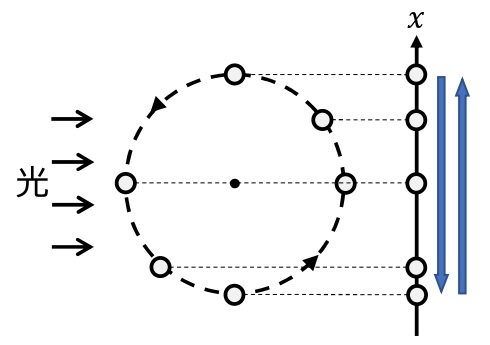
単振動の変位・速度・加速度
運動方程式：\(ma=-Kx\)
変位：\(x=A\sin\omega t\)
速度：\(v=A\omega\cos\omega t\)
変位：\(a=-A\omega^2\sin\omega t=-\omega^2x\)
周期：\(\displaystyle T=2\pi\sqrt{\frac{m}{K}}\)
質量\(m\)[kg]，振幅\(A\)[m]，角振動数\(\omega\)[rad/s]，時間\(t\)[s]，変位\(x\)[m]，速度\(v\)[m/s]，加速度\(a\)[m/s²]
単振動の変位
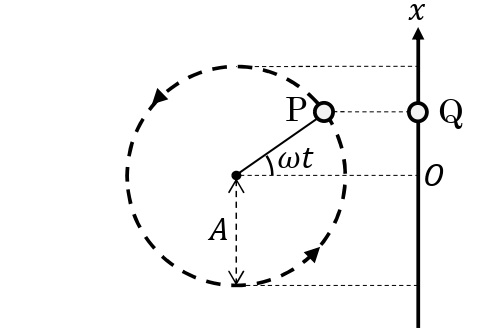
物体Pが，半径\(A\)[m]の円周上を角速度\(\omega\)[rad/s]で等速円運動している。物体Pから\(x\)軸に下した垂線の交点をQとしたとき，Qが原点を上向きに通過する時刻を\(0\)とすると，時刻\(t\)[s]における点Qの位置\(x\)[m]は，
\begin{eqnarray}x=A\sin\omega t \cdots\cdots\cdots①\end{eqnarray}
とあらわすことができる。このとき，振動の中心から振動の端までの距離は\(A\)[m]であらわすことができ，これを振幅と呼ぶ。また，\(\omega\)[rad/s]を角振動数，\(\theta=\omega t\)を時刻\(t\)[s]における位相と呼ぶ。
1回の振動に要する時間\(T\)[s]を周期，1秒当たりの往復回数\(f\)[Hz]を振動数という。単振動における角振動数，周期，振動数は，等速円運動におけるの角速度，周期，回転数に相当しているので，
\begin{eqnarray}f=\dfrac{1}{T} T=\dfrac{2\pi}{\omega}\end{eqnarray}
の関係が成り立つ。
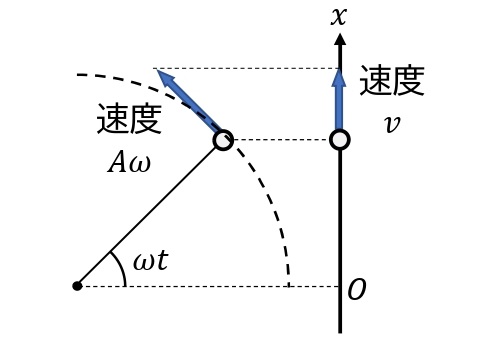
単振動の速度・加速度
Qの速度\(v\)[m/s]は，等速円運動しているPの速度の\(x\)成分で表すことができるので，下図より，
\begin{eqnarray}v=A\omega\cos\omega t \cdots\cdots\cdots②\end{eqnarray}
となる。
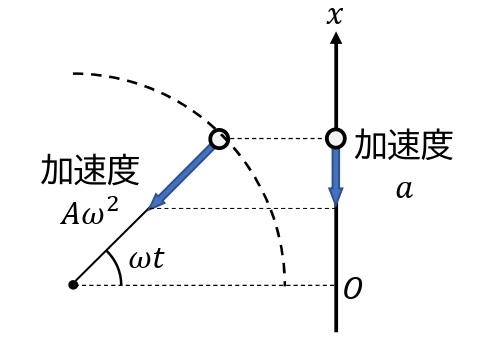
速度と同様に，Qの加速度\(a\)[m/s²]は，等速円運動しているPの加速度の\(x\)成分で表すことができるので，下図より，
\begin{eqnarray}a=-A\omega^2\sin\omega t \cdots\cdots\cdots③\end{eqnarray}
となる。また，①，③より，
\begin{eqnarray}a=-\omega^2 x \cdots\cdots\cdots④\end{eqnarray}
が得られる。
復元力
質量\(m\)[kg]の物体が\(x\)軸上を角速度\(\omega\)[rad/s]で単振動するとき，物体が受ける力を\(F\)[N]とする。運動方程式「\(ma=F\)」と④より，\(F\)は，
\begin{eqnarray}F=ma=-m\omega^2x\end{eqnarray}
とあらわすことができる。ここで，定数\(m\omega^2=K\)とすると，上の式\(F\)は，
\begin{eqnarray}F=-Kx\end{eqnarray}
と書くことができる。単振動をする物体が受ける力\(F\)は，変位\(x\)の大きさに比例し，常に変位と逆向きつまり振動の中心を向いていることがわかる。この力を復元力という。ちなみに，\(F=-Kx\)と\(F=-m\omega^2x\)を比較すると，
\begin{eqnarray}\omega=\sqrt{\dfrac{K}{m}}\end{eqnarray}
とあらわすことができるので，単振動の周期\(T\)[s]は，
\begin{eqnarray}T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{K}}\end{eqnarray}
となる。
ばね振り子
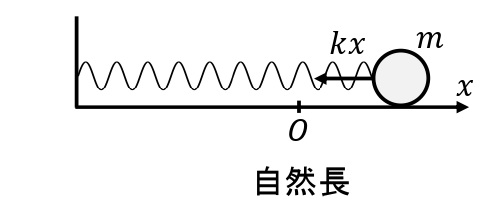
水平ばね振り子
なめらかな水平面上にばね定数\(k\)のばねの一端を固定し，質量\(m\)[kg]のおもりをつけて振動させる。ばねが自然長の位置を原点とし，ばねが伸びる向きを正とする。変位が\(x\)[m]のときおもりの運動方程式は，
\begin{eqnarray}ma=-kx\end{eqnarray}
とあらわすことができる。したがって，おもりは点Oを中心とする周期\(T=2\pi\sqrt{\dfrac{m}{k}}\)の単振動であることがわかる。
鉛直ばね振り子
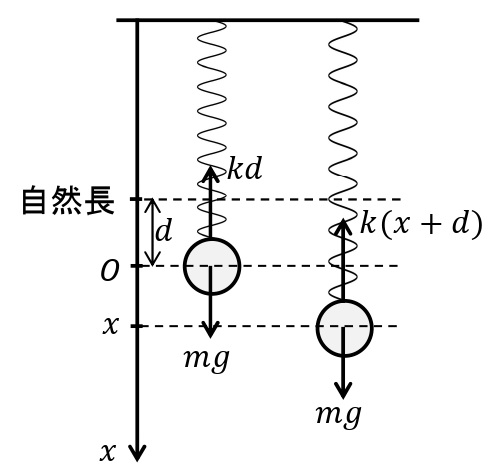
ばね定数\(k\)のばねの一端を天井に固定し，質量\(m\)[kg]のおもりをもう一方の端に吊り下げた。おもりがつり合いの位置で静止しているときのばねの伸びを\(d\)[m]とすると，
\begin{eqnarray}kd=mg\end{eqnarray}
が成り立つ。つりあいの位置を原点とし，ばねが伸びる向きを正とする。おもりの位置が\(x\)[m]のときおもりの運動方程式は，
\begin{eqnarray}ma=-k(x+d)+mg=-kx\end{eqnarray}
とあらわすことができる。したがって，おもりはつりあいの位置を中心とする周期\(T=2\pi\sqrt{\dfrac{m}{k}}\)の単振動であることがわかる。
単振り子
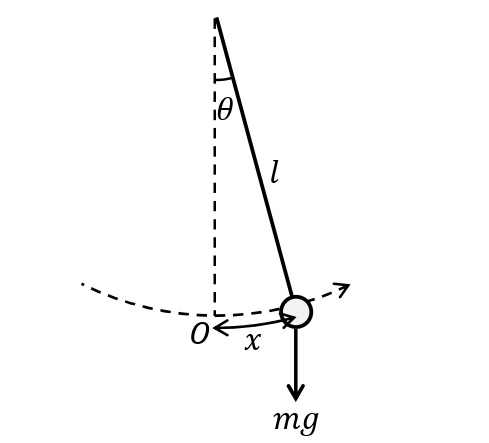
軽い糸におもりをつるして，鉛直面内で振動させたものを単振り子という。振動の振れの角度が小さいとき，単振り子の運動は単振動とみなすことができる。
最下点をOとし，おもりの点Oからの円弧に沿った変位を\(x\)[m]（反時計まわりを正），糸の長さを\(l\)[m]，おもりの質量\(m\)[kg]とする。おもりの円弧に沿った方向の力\(F\)[N]は，
\begin{eqnarray}F=-mg\sin\theta\end{eqnarray}
とあらわすことができる。ここで，\(\theta\)が十分小さいとき，\(\sin\theta≒\theta\)で近似できるので，
\begin{eqnarray}F≒-mg\theta\end{eqnarray}
となる。\(x=l\theta\)より，
\begin{eqnarray}F≒-mg\dfrac{x}{l}\end{eqnarray}
が成り立つ。したがって，おもりは，\(F\)が復元力となって単振動しているとみなすことができる。その振動の周期\(T\)[s]は，\(K=\dfrac{mg}{l}\)とおけば，周期の公式\(T=2\pi\sqrt{\dfrac{m}{K}}\)より，\(T=2\pi\sqrt{\dfrac{l}{g}}\)となる。
コメント