本記事では、『光の干渉~ヤングの実験・回折格子・薄膜の干渉・くさび形・ニュートンリング~』について解説していきたいと思います。
物理講師ともくん

経歴 東北大学物理学科→東北大学大学院理学研究科物理学専攻→公務員(教職ではない)→塾業界に転職→3つの予備校&塾をかけもつプロ講師(物理・数学)
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
ヤングの実験
光源から出た単色光をスリットS\(_0\)に通すと,光が回折し,その後,2つのスリットS\(_1\),S\(_2\)を通ってて回折した光がスクリーン上で強めあったり,弱めあったりして,スクリーンに明暗の縞模様ができる。この縞を干渉縞という。
単色光の波長を\(\lambda\),スリットS\(_1\),S\(_2\)の間隔を\(d\),スクリーン上の点PからOまでの距離を\(x\)とする。Pに至る二経路の経路差は\(\displaystyle|l_1-l_2|≒\frac{dx}{l}\)と表される。よって,水面波の干渉と同様に,干渉によって強めあってできる明るい線(明線),弱めあってできる暗い線(暗線)ができる条件は,整数\(m\)を用いて次のように表すことができる。
\begin{eqnarray}\displaystyle&&明線:\frac{dx}{l}=m\lambda (m=0,1,2,\cdots)\\ &&暗線:\frac{dx}{l}=\left(m+\frac{1}{2}\right)\lambda (m=0,1,2,\cdots) \end{eqnarray}
また,隣りあう明線(暗線)の間隔を\(\it\Delta x\)とすると,明線の条件式より,次の関係が成り立つ。
\begin{eqnarray}\displaystyle\it\Delta x&=&(m+1)\frac{l\lambda}{d}-m\frac{l\lambda}{d}\\ &=&\frac{l\lambda}{d} \end{eqnarray}
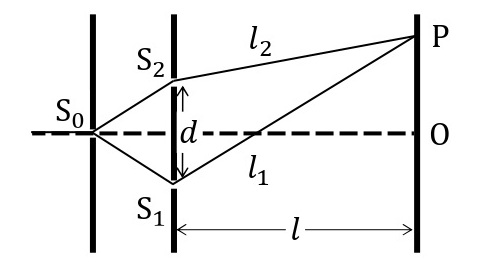
<経路差の求め方>
スリットS\(_1\),S\(_2\)からPまでの経路差は,次のように求められる。
\begin{eqnarray}\displaystyle|l_1-l_2|&=&\sqrt{l^2+\left(x+\frac{d}{2}\right)}-\sqrt{l^2+\left(x-\frac{d}{2}\right)}\\ &=&l\sqrt{1+\frac{\left(x+\frac{d}{2}\right)^2}{l^2}}-l\sqrt{1+\frac{\left(x-\frac{d}{2}\right)^2}{l^2}} \end{eqnarray}
ここで,\(d\),\(x\)は\(l\)に比べてきわめて小さいので,\(|a|\ll1\)のとき成り立つ近似式\(\displaystyle\sqrt{1+a}≒1+\frac{1}{2}a\)を用いると,
\begin{eqnarray}\displaystyle|l_1-l_2|&≒&l\left\{1+\frac{1}{2}\cdot\frac{\left(x+\frac{d}{2}\right)^2}{l^2}\right\}-l\left\{1+\frac{1}{2}\cdot\frac{\left(x-\frac{d}{2}\right)^2}{l^2}\right\}\\&=&\frac{dx}{l} \end{eqnarray}
回折格子
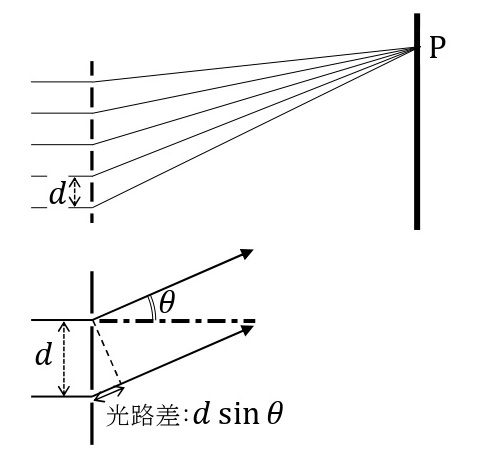
ガラス板に多くの平行な細い溝を等間隔でつけたものを回折格子という。溝の部分は光は透過できないため,溝と溝の間がスリットとして機能することになる。回折格子に光を当てると,これらのスリットから出た光は回折し,互いに干渉する。
溝と溝の間隔(格子定数)が\(d\)である回折格子に波長\(\lambda\)の光を垂直に入射する。回折格子から十分に遠方のスクリーン上の点Pに向かう光はほぼ平行とみなすことができる。この光が入射光となす角を\(\theta\)とすると,隣りあう光の経路差は\(d\sin\theta\)と表される。よって,\(\theta\)の方向で光が強めあって明るくなる条件は次のようになる。
\begin{eqnarray}\displaystyle d\sin\theta=m\lambda (m=0,1,2,\cdots) \end{eqnarray}
薄膜による干渉
シャボン玉や水面上の油膜などの薄膜は,色づいて見える。これは,膜の表面で反射した光と,膜の裏面で反射した光とが干渉するためである。
反射光の位相
屈折率の小さい媒質から入射し,屈折率の大きい媒質との境界面で反射するとき,反射によって位相が反転する(\(\pi\)だけ変化する)。一方,屈折率の大きい媒質から入射し,屈折率の小さい媒質との境界面で反射するとき反射によって位相は変化しない。
光路長
屈折率\(n\)の媒質中では,光速は真空中の\(\displaystyle\frac{1}{n}\)倍となる。光がこの媒質中を距離\(L\)だけ進むのにかかる時間で,真空中では距離\(nL\)進むことになる。この\(nL\)を光路長という。
薄膜による光の干渉
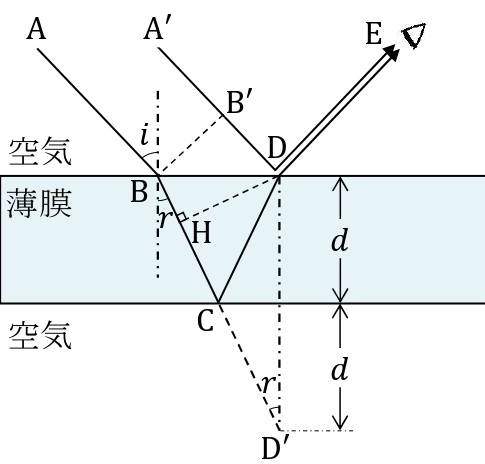
屈折率\(n\),厚さ\(d\)の薄膜に,光が入射角\(i\)で斜めに入射する場合を考える。このとき,A\(‘\)→B\(‘\)→D→Eのように薄膜の上面で反射して観測する光①と,A→B→C→D→Eのように薄膜の下面で反射する光②に着目する。入射波の波面BB\(‘\)を経た後,屈折して膜の中に入り,HD上に来る。よって,光①と光②の経路差は\(\rm HC+CD\)であり,屈折角を\(r\)とすると,
\begin{eqnarray}\rm HC+CD=HC+CD’=HD’=2\it d\cos r \end{eqnarray}
とあらわされる。薄膜の屈折率は\(n\)であるので,光路差は\(2nd\cos r\)となる。また,光①は点Dにおける反射で位相が反転し,光②は点Cにおける反射で位相は変化しないので,反射光が強めあう条件は次のようになる。
\begin{eqnarray}\displaystyle 2nd\cos r=\left(m+\frac{1}{2}\right)\lambda (m=0,1,2,\cdots) \end{eqnarray}
くさび形空気層における光の干渉
長さ\(L\)の2枚の平面ガラスを重ねて一端に厚さ\(D\)の薄い紙をはさみ,くさび形の空気層を作る。このとき,真上から単色光を入射させると,明暗の縞模様が見える。これは,上のガラスの下面で反射する光と,下のガラスの上面で反射する光とが干渉するためである。
点Oを基準とした位置\(x\)における空気層の厚さを\(\displaystyle d\left(=\frac{Dx}{L}\right)\)とすると,上のガラスの下面で反射する光と,下のガラスの上面で反射する光の経路差は\(\displaystyle 2d\left(=\frac{2Dx}{L}\right)\)と表される。ガラスは空気より屈折率が大きいので,上のガラスの下面で反射する光は反射の際に位相が変化しないが,下のガラスの上面で反射する光は反射の際に位相が反転する。以上より,単色光の波長を\(\lambda\)とすると干渉の条件式は次のようになる。
\begin{eqnarray}\displaystyle &&明線:2d=\frac{2Dx}{L}=\left(m+\frac{1}{2}\right)\lambda (m=0,1,2,\cdots)\\ &&暗線:2d=\frac{2Dx}{L}=m\lambda (m=0,1,2,\cdots) \end{eqnarray}
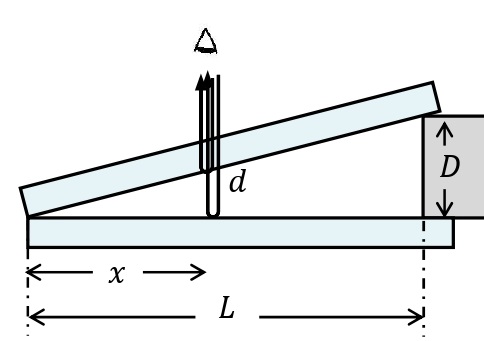
<空気層の厚さ\(d\)の求め方>
\(D\)は\(L\)に対して非常に小さく,光はほぼ真上に反射する。三角形の相似の関係より,
\begin{eqnarray}\displaystyle L:D&=&x:d\\ Ld&=&Dx\\ d&=&\frac{Dx}{L} \end{eqnarray}
ニュートンリング
一方が平面で,他方が半径\(R\)の球面のできている平凸レンズを平面ガラスの上にのせる。上から平面に垂直に単色光を当てると,レンズと平面ガラス板との接点を中心とする同心円状の明暗の縞模様が見える。これは,レンズの下面で反射する光と,ガラスの上面で反射する光とが干渉するためである。この縞模様をニュートンリングという。
レンズと平面ガラス板との接点からの距離を\(x\)におけるレンズとガラスの間の空気層の厚さを\(\displaystyle d\left(=\frac{x^2}{2R}\right)\)とすると,レンズの下面で反射する光と,ガラスの上面で反射する光の経路差は\(\displaystyle 2d\left(=\frac{x^2}{R}\right)\)と表される。レンズ,ガラスは空気より屈折率が大きいので,レンズの下面で反射する光は反射の際に位相が変化しないが,ガラスの上面で反射する光は反射の際に位相が反転する。以上より,単色光の波長を\(\lambda\)とすると干渉の条件式は次のようになる。
\begin{eqnarray}\displaystyle &&明線:2d=\frac{x^2}{R}=\left(m+\frac{1}{2}\right)\lambda (m=0,1,2,\cdots)\\ &&暗線:2d=\frac{x^2}{R}=m\lambda (m=0,1,2,\cdots) \end{eqnarray}
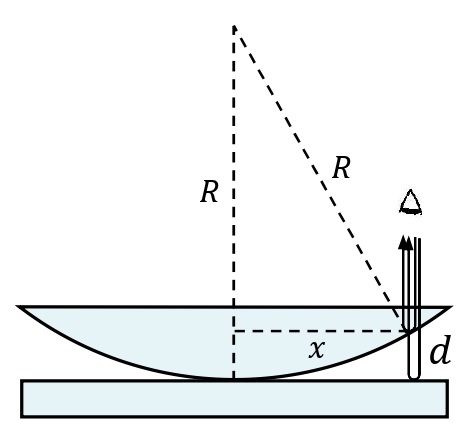
<空気層の厚さ\(d\)の求め方>
\(d\)は\(R\)に対して非常に小さく,光はほぼ真上に反射する。三平方の定理より,
\begin{eqnarray}\displaystyle R^2&=&(R-d)^2+x^2\\ &=&R\left(1-\frac{d}{R}\right)^2+x^2\\ &≒&R^2\left(1-\frac{2d}{R}\right)+x^2 \end{eqnarray}
よって,\(\displaystyle 2d=\frac{x^2}{R}\)となる。なお,ここで\(x\ll1\)のとき,\((1+x)^n≒1+nx\)を用いた。










コメント