【高校物理の要点】気体の分子運動～分子運動と圧力・平均運動エネルギーと二乗平均速度～

本記事では、『気体の分子運動～分子運動と圧力・平均運動エネルギーと二乗平均速度～』について解説していきたいと思います。

分子運動と圧力

分子運動と圧力：\(\displaystyle p=\frac{Nm\overline{v^2}}{3V}\)

圧力\(p\)[Pa]，体積\(V\)[m³]，気体分子の個数\(N\)[個]，質量\(m\)[kg]，分子の速度の2乗の平均値\(\overline{v^2}\)[m/s]

1辺の長さ\(L\)[m]の立方体の容器に，質量\(m\)[kg]の理想気体の気体分子\(N\)個入っている。下図のように\(x\)，\(y\)，\(z\)軸をとり，\(x\)軸に垂直な壁Aが受ける圧力を考える。分子は，他の分子とは衝突せず，分子と壁との衝突は弾性衝突とする。

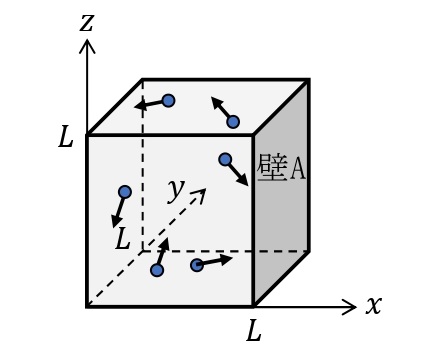
1回の衝突で壁Aが分子から受ける力積

壁Aに衝突する直前の分子の速度を\(\overrightarrow{v}=(v_x，v_y，v_z)\)とする。弾性衝突より，壁Aに垂直な成分のみ向きが変わるので，衝突直後の分子の速度は\(\overrightarrow{v’}=(-v_x，v_y，v_z)\)となる。このとき分子の運動量の変化，すなわち，分子が壁Aから受ける力積は，

\begin{eqnarray}m\overrightarrow{v’}-m\overrightarrow{v}&=&(-2mv_x，0，0)\end{eqnarray}

であらわされる。作用反作用の法則より，分子が壁Aに与える力積は壁と垂直な向き(\(x\)軸の正の向き)で大きさは\(2mv_x\)[N・s]となる。

分子が再び壁Aと衝突するまでの時間

\(x\)軸方向のみに着目すると，壁Aと衝突した分子は，1往復で再度壁Aと衝突するので，衝突の周期は\(\dfrac{2L}{v_x}\)となる。

壁Aが1つの分子から受ける平均の力

壁Aは，1つの分子から\(\dfrac{2L}{v_x}\)の周期で大きさ\(2mv_x\)の力積を受ける。時間\(t\)[s]の間に分子が壁Aに衝突する回数は

\begin{eqnarray}\dfrac{2L}{v_x}秒：1回&=&t秒：n回\\n&=&\dfrac{v_xt}{2L}\end{eqnarray}

となるので，分子から受ける力積の合計は

\begin{eqnarray}I&=&2mv_x\times\dfrac{v_xt}{2L}=\dfrac{mv_x^2}{L}t\end{eqnarray}

となる。この分子によって壁Aが受ける平均の力の大きさを\(\overline{f}\)[N]とすると，\(I=\overline{f}t\)より，

\begin{eqnarray}\overline{f}t&=&\dfrac{mv_x^2}{L}t\\ \overline{f}&=&\dfrac{mv_x^2}{L}\end{eqnarray}

と表すことができる。

壁Aが\(N\)個の分子から受ける圧力

壁Aが\(N\)個の分子から受ける平均の力の大きさ\(F\)[N]は，気体分子全体の\(v_x^2\)の平均を\(\overline{v_x^2}\)とすると，

\begin{eqnarray}F&=&N\times\dfrac{m\overline{v_x^2}}{L}\end{eqnarray}

となる。ここで，全分子の速度の2乗の平均値\(\overline{v^2}\)を三平方の定理を用いて各成分の2乗の平均値で表すと，\(\overline{v^2}=\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2}\)の関係が成りたつ。また，分子の個数\(N\)はきわめて大きく，すべての分子はランダムに運動している。よって，どの方向の平均値も等しく，\(\overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}\)と考えることができる。以上から\(\overline{v_x^2}=\dfrac{1}{3}\overline{v^2}\)が導かれる。よって，

\begin{eqnarray}F&=&N\times\dfrac{m\overline{v_x^2}}{L}=\dfrac{Nm\overline{v^2}}{3L}\end{eqnarray}

となる。

気体の圧力\(p\)[Pa]は，\(F\)を壁Sの面積\(S\)[m²]でわれば求められる。\(L^3=V\)を用いると，\(p\)は次のように表される。

\begin{eqnarray}p=\dfrac{F}{L^2}&=&\dfrac{Nm\overline{v^2}}{3L^3}=\dfrac{Nm\overline{v^2}}{3V}\end{eqnarray}

平均運動エネルギーと二乗平均速度

平均運動エネルギー

平均運動エネルギー：\(\dfrac{1}{2}m\overline{v^2}=\dfrac{3}{2}kT\)

質量\(m\)[kg]，分子の速度の2乗の平均値\(\overline{v^2}\)[m/s]，ボルツマン定数\(k\)[J/K]，温度\(T\)[K]

\(p=\dfrac{Nm\overline{v^2}}{3V}\)と理想気体の状態方程式\(pV=nRT\)より，

\begin{eqnarray}\dfrac{Nm\overline{v^2}}{3}=nRT\end{eqnarray}

の関係が得られる。これを用いて，気体分子の平均運動エネルギーを求める。気体分子の個数\(N\)は，分子量\(n\)[mol]とアボガドロ定数\(N_A\)を用いると，\(N=nN_A\)であるので，

\begin{eqnarray}\dfrac{1}{2}m\overline{v^2}&=&\dfrac{3nRT}{2N}\\&=&\dfrac{3}{2}\times\dfrac{R}{N_A}\times T\\&=&\dfrac{3}{2}kT\end{eqnarray}

と表される。以上から理想気体では平均運動エネルギーが気体の種類によらず，温度だけで決まり，絶対温度に比例することがわかる。ここで，定数\(k\)は，気体定数\(R\)をアボガドロ定数\(N_A\)でわったもので，ポルツマン定数という。

二乗平均速度

二乗平均速度：\(\sqrt{\overline{v^2}}=\sqrt{\dfrac{3RT}{mN_A}}\)

二乗平均速度\(\sqrt{\overline{v^2}}\)[m/s]，質量\(m\)[kg]，アボガドロ定数\(N_A\)[1/mol]}
気体定数\(R\)[(J・K)/mol]，温度\(T\)[K]

\(\dfrac{1}{2}m\overline{v^2}=\dfrac{3}{2}\times\dfrac{R}{N_A}\times T\)の式より，

\begin{eqnarray}\sqrt{\overline{v^2}}=\sqrt{\dfrac{3RT}{mN_A}}\end{eqnarray}

となる。以上から理想気体では二乗平均速度は気体の種類と温度によって決まることがわかる。