【高校物理の要点】気体の状態変化～熱力学第一法則/定圧変化/定積変化/等温変化/断熱変化～

本記事では、『気体の状態変化』について解説していきたいと思います。

単原子分子理想気体の内部エネルギー

単原子分子理想気体の内部エネルギー：\(\displaystyle U=\frac{3}{2}nRT\)

単原子分子理想気体の内部エネルギー\(U\)[J]，物質量\(n\)[mol]，気体定数\(R\)[(J・K)/mol]，温度\(T\)[K]

一般に，気体の内部エネルギーは，気体分子の熱運動による運動エネルギーと分子間力による位置エネルギーの和である。理想気体では，分子間にはたらく力は無視できるので，位置エネルギーは\(0\)とすることができる。したがって，内部エネルギーは熱運動による運動エネルギーの合計と考えてよい。気体の平均運動エネルギーは\(\displaystyle\frac{1}{2}m\overline{v^2}=\frac{3}{2}\frac{R}{N_A}T\)とあらわされることから，\(\displaystyle n=\frac{N}{N_A}\)[mol]の単原子分子理想気体の内部エネルギー\(U\)[J]は，次のようになる。

\begin{eqnarray}U&=&N\times\frac{1}{2}m\overline{v^2}\\&=&nN_A\times\frac{3}{2}\frac{R}{N_A}T\\&=&\frac{3}{2}nRT\end{eqnarray}

熱力学第一法則

熱力学第一法則：\(Q_吸=\it\Delta U+W_{\rm した}\)

内部エネルギーの変化\(\it\Delta U\)[J]，気体が受け取った熱量\(Q_吸\)[J]，外部にした仕事\(W_{\rm した}\)[J]

気体が受け取った熱量\(Q_吸\)[J]のとき，内部エネルギーが\(\it\Delta U\)[J]だけ変化し，外部に\(W_{\rm した}\)[J]だけ仕事をする場合，次の式が成り立つ。

\begin{eqnarray}Q_吸&=&\it\Delta U+W_{\rm した}\end{eqnarray}

ただし，\(Q_吸\)，\(\it\Delta U\)，\(W_{\rm した}\)の符号と物理的な意昧の関係は，次のとおりである。

• 熱を吸収するとき\(Q_吸>0\)，放出するとき\(Q_吸<0\)
• 内部エネルギーが増加（\(\it\Delta T>\rm0\)）するとき\(\it\Delta U>\rm0\)，減少（\(\it\Delta T<\rm0\)）するとき\(\it\Delta U<\rm0\)
• 外部に仕事をする（気体の体積が増加）とき\(W_{した}>0\)，外部から仕事をされる（気体の体積が減少）とき\(W_{した}<0\)

気体がする仕事

気体がする仕事：\(W_{した}=p\it\Delta V\)

外部にした仕事\(W_{した}\)[J]，圧力\(p\)[Pa]，微小体積変化\(\it\Delta V\)[m³]

圧力\(p\)[Pa]の気体が断面積\(S\)[m²]のシリンダーにピストンで封じられているとする。ここで，ピストンを微小距離\(\it\Delta x\)[m]だけ動かす。気体はピストンに対して，大きさ\(F=pS\)[N]の力を加えているので，\(\it\Delta V=S\it\Delta x\)を用いると，気体が外部にする仕事は，次のようになる。

\begin{eqnarray}W_{した}&=&F\it\Delta x\\&=&pS\it\Delta x\\&=&p\it\Delta V\end{eqnarray}

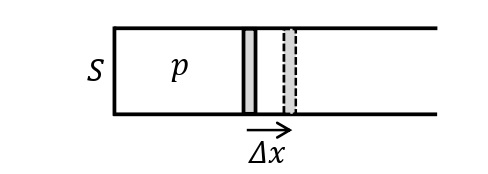
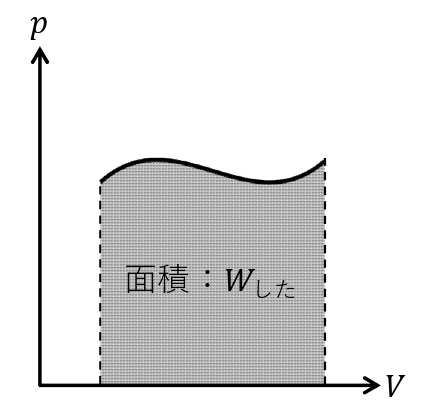
気体の状態変化を表す便利なグラフとして, 縦軸に圧力\(p\)，横軸に体積\(V\)をとった\(p\)-\(V\)グラフが知られている。気体がした仕事の大きさは\(p\)-\(V\)グラフと\(V\)軸で囲まれる部分の面積に等しい。

気体の状態変化

気体の状態変化
理想気体の状態変化のうち，代表的なもとして，定積変化，定圧変化，等温変化，断熱変化があげられる。

　定積変化 ：体積が一定の状態変化。気体が外部にする仕事\(W_{した}=0\)である。

　定圧変化 ：圧力が一定の状態変化。気体が外部にする仕事は\(W_{した}=p\it\Delta V\)であらわされる。

　等温変化 ：温度が一定の状態変化。気体の内部エネルギーの変化量\(\it\Delta U=\rm0\)である。

　断熱変化 ：外部と熱のやりとりがない状態変化。気体の吸収する熱量\(Q_{吸}=0\)である。

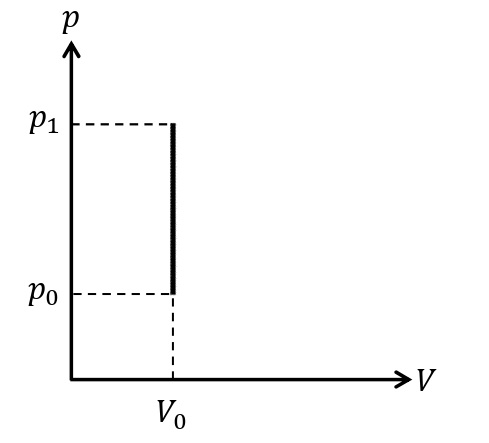
定積変化

体積一定の変化を定積変化(または等積変化)という。定積変化において\(\it\Delta V=\rm0\)より気体は外部に仕事しないので，与えた熱量だけ気体の内部エネルギーが増加する。

\begin{eqnarray}&&W_{した}=0\\&&Q_{吸}=\it\Delta U\end{eqnarray}

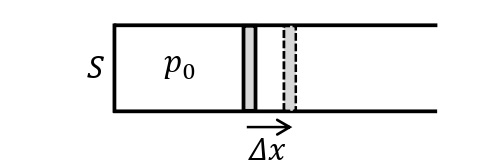
定圧変化

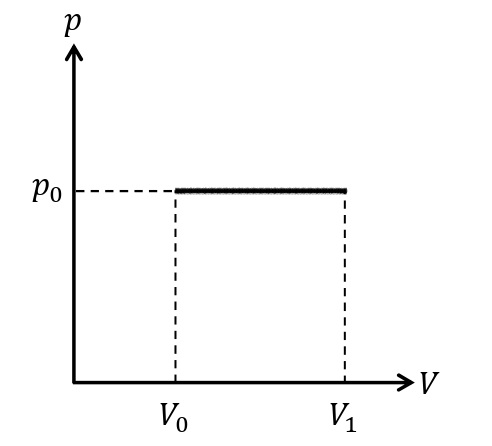
圧力一定の変化を定圧変化(または等圧変化)という。ピストンが自由に動ける状態の円筒内のシリンダーに気体を封印し，圧力一定条件下で気体に熱量\(Q_{吸}\)[J]を加える。気体の圧力を\(p_0\)[Pa]，ピストンの断面積を\(S\)[m²]とすると，気体は一定の大きさの力\(p_0S\)[N]でピストンを押す。ここで，ピストンが\(\it\Delta x\)[m]移動したとすると，気体が外部にした仕事\(W_{した}\)は，\(\it\Delta V=S\it\Delta x\)[m³]を用いると，\(W_{した}=p_0S\it\Delta x=p_{\rm0}\it\Delta V\)であらわされる。よって，熱力学第一法則より，以下の式が成り立つ。

\begin{eqnarray}Q_{吸}=\it\Delta U+p_{\rm0}\it\Delta V\end{eqnarray}

等温変化

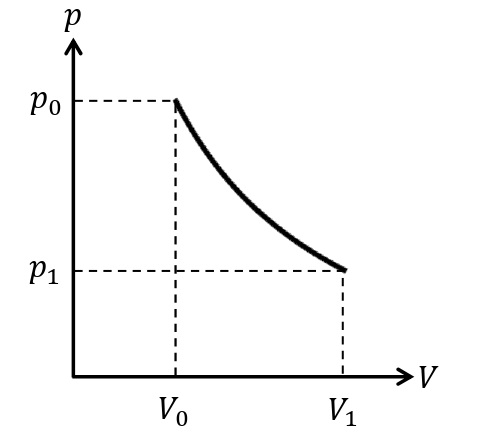
温度一定の変化を等温変化という。ボイルの法則より，気体の圧力は体積に反比例する。等温変化では，気体の内部エネルギーに変化はないので，

\begin{eqnarray}&&\it\Delta U=\rm0\\&&Q_{吸収}=W_{した}\end{eqnarray}

が成りたつ。等温変化では気体が吸収した熱量をすべて膨張によってした仕事に使う。

断熱変化

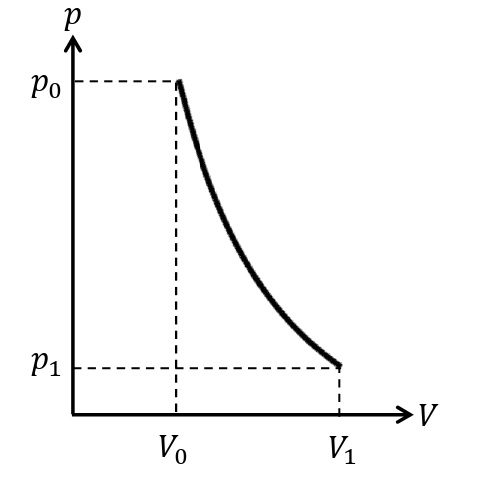
外部との熱のやりとりがないよう変化を断熱変化という。このとき，

\begin{eqnarray}&&Q_{吸収}=0\\&&0=\it\Delta U\rm +\it W_{\rm した}\end{eqnarray}

が成りたつ。気体を断熱膨張させるとき，気体がした仕事\(W_{した}\)は正であるので，\(0=\it\Delta U\rm+\it W_{\rm した}\)の式より\(\it\Delta U<\rm0\)である。ゆえに，内部エネルギーが減少するので，温度が下がる。

モル比熱

物質\(1\)molの温度を\(1\)K高めるのに必要な熱量をモル比熱という。物質\(n\)[mol]の温度を\(\it\Delta T\)[K] 高めるのに必要な熱量\(Q\)[J]は，モル比熱\(C\)[J/(mol・K)]を用いて

\begin{eqnarray}Q=nC\it\Delta T\end{eqnarray}

と表される。

定積モル比熱

気体が定積変化するときのモル比熱を定積モル比熱といい，\(C_V\)[J/(mol・K)]で表す。定積変化の場合，気体が吸収した熱はすべて内部エネルギーの増加になるので，

\begin{eqnarray}\it\Delta U\rm=\it nC_V\it\Delta T\end{eqnarray}

が成り立つ。

定圧モル比熱

気体が定圧変化するときのモル比熱を定圧モル比熱といい，\(C_p\)[J/(mol・K)]で表す。定圧変化の場合，理想気体の状態方程式\(p\it\Delta V=nR\it\Delta T\)より，

\begin{eqnarray}C_p&=&\dfrac{Q}{n\it\Delta T}\\&=&\dfrac{\it\Delta U}{n\it\Delta T}+\dfrac{p\it\Delta V}{n\it\Delta T}\\&=&\dfrac{\it\Delta U}{n\it\Delta T}+R\end{eqnarray}

が成り立つ。\(C_V=\dfrac{\it\Delta U}{n\it\Delta T}\)より，次の関係式が得られる。これをマイヤーの関係という。

\begin{eqnarray}C_p=C_V+R\end{eqnarray}

単原子分子理想気体のモル比熱

単原子分子理想気体においては，内部エネルギーの変化の式\(\it\Delta U=\rm\dfrac{3}{2}\it nR\it\Delta T\)と表される。定積変化では\(\it\Delta U=Q_{\rm 吸}\)であるので，

\begin{eqnarray}C_V=\dfrac{Q_{吸}}{n\it\Delta T}=\dfrac{\it\Delta U}{n\it\Delta T}=\dfrac{3}{2}R\end{eqnarray}

となる。また，マイヤーの関係式より，

\begin{eqnarray}C_p=C_V+R=\dfrac{5}{2}R\end{eqnarray}

と表される。

比熱比

定圧モル比熱\(C_p\)と定積モル比熱\(C_V\)の比\(\gamma=\dfrac{C_p}{C_V}\)のことを比熱比という。また，単原子分子理想気体では\(\gamma=\dfrac{5/2}{3/2}=\dfrac{5}{3}\)が成りたつ。理想気体では，断熱変化するときの圧力\(p\)[Pa]と体積\(V\)[m³]には

\begin{eqnarray}pV^\gamma=一定\end{eqnarray}

の関係があることが知られている。これをポアソンの法則という。