本記事では、『電場と電位~クーロンの法則・点電荷による電場,電位・ガウスの法則~』について解説していきたいと思います。

予備校講師ともくん
専門科目:物理
経歴:東北大学物理学科
→東北大学大学院理学研究科物理学専攻
→公務員(教職ではない)
→塾業界に転職
→予備校&塾に出講中のプロ講師
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
静電気力
静電気
物体が電気を帯びることを帯電という。帯電している物体(帯電体)がもつ電気を電荷という。大きさが無視できる点状の電荷を点電荷という。静止した電荷の間には力がはたらきこれを静電気力という。電荷には正電荷と負電荷の2種類あり,同符号の電荷は互いに斥力を,異符号の電荷は互いに引力を及ぼしあう。電荷の量を電気量といい単位にはクーロン(記号C)を用いる。
電気量保存の法則
物体間で電荷の移動があっても移動の前後で電気量の総和は変わらない。これを電気量保存の法則という。
クーロンの法則
クーロンの法則:\(\displaystyle F=k\frac{|q_1|\cdot|q_2|}{r^2}\)
静電気力の大きさ\(F\)[N],クーロンの法則の比例定数\(k\)[N・m²/C²],2つの点電荷の電気量の大きさ\(|q_1|\),\(|q_2|\)[C],点電荷間の距離\(r\)[m]
電気量の大きさ\(q_1\),\(q_2\)[C]の2つの点電荷の間にはたらく静電気力の大きさ\(F\)[N]は,それぞれの電気量の大きさ\(q_1\)と\(q_2\)に比例し,点電荷の間の距離\(r\)[m]の2乗に反比例する。これをクーロンの法則という。比例定数を\(k\)(≒\(9.0\times10^9\)N・m²/C²)とすると,\(\displaystyle F=k\frac{|q_1|\cdot|q_2|}{r^2}\)の式で表される。
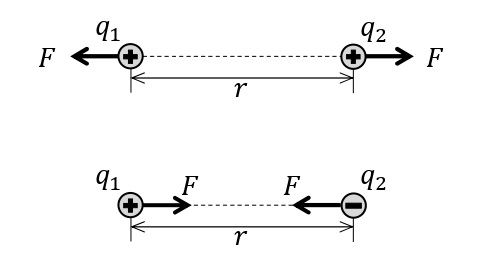
導体と不導体
金属内部には自由に動くことのできる電子(自由電子)が存在しているので,電気を良く通す。このように電気を良く通す物質を導体という。一方,電気をほとんど通さない物質を不導体(絶縁体,誘電体ともいう)という。
導体の静電誘導
導体に帯電体を近づけると,自由電子が静電気力によって速やかに移動する。そのため,帯電体に近い側の表面には帯電体と異種の電気が現れ,遠い側の表面には帯電体と同種の電気が現れる。この現象を導体の静電誘導という。
不導体の静電誘導
不導体に帯電体を近づけた場合でも,導体の場合と同様に電荷が現れる。これは,静電気力によって構成粒子に属している電子の位置がずれ,電子分布に偏りが生じるためである。この現象を誘電分極という。
電場
電場
電荷が電場から受ける力:\(\overrightarrow{F}=q\overrightarrow{E}\)
静電気力\(\overrightarrow{F}\)[N],電気量\(q\)[C],電場\(\overrightarrow{E}\)[N/C]
クーロン力のはたらく空間を電場または電界という。ある場所の電場は,その場所に置いた単位電荷(+1C)あたりが受ける力として定義される。その単位はN/Cを用いる。
電場は力と同様に,大きさと向きをもつベクトル(電場ベクトル)である。正電荷は電場の向きに力を受け,負電荷は電場と逆向きに力を受ける。電場ベクトル\(\overrightarrow{E}\)の点に電気量\(q\)[C]の点電荷を置いたとき,この点電荷にはたらく力\(\overrightarrow{F}\)[N]は\(\overrightarrow{F}=q\overrightarrow{E}\)で表される。
点電荷のまわりの電場
点電荷のまわりの電場:\(\displaystyle E=k\frac{Q}{r^2}\)
電場の強さ\(E\)[N/C],クーロンの法則の比例定数\(k\)[N・m²/C²],点電荷の電気量の大きさ\(Q\)[C],点電荷からの距離\(r\)[m]
空間内に\(+Q\)[C]の正電荷が存在するとき,点電荷から離れる方向に電場が生じる。点電荷から\(r\)[m]離れた場所での電場の大きさを\(E\)とすると,クーロンの法則から,\(\displaystyle E=k\frac{Q}{r^2}\)と表される。空間内に\(-Q\)[C]の負電荷が存在するとき,点電荷に近づく方向に電場が生じ,電場の強さは正電荷の場合と同様に上記の式で表される。
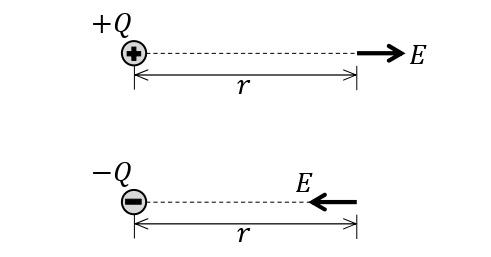
電気力線
電場の中に置かれた正電荷が受ける力の軌跡を電気力線という。電気力線には次のような性質がある。
- 電気力線は正電荷から出て負電荷に入る。
- 電気力線上の各点での接線は,その点での電場の方向と一致する。
- 電気力線は折れ曲がったり,枝分かれしたり,交差したりしない。
- 電場の強さが\(E\)[N/C]の点では,1m²当たり\(E\)本の割合で電気力線が面を垂直に貫く。電場が強い所ほど電気力線は密であり,電場の弱い場所では疎である。
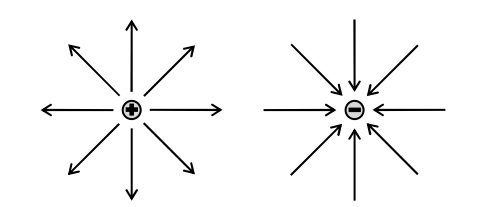
帯電体から出る電気力線の数
電場の強さが\(E\)[N/C]の点では,1m²当たり\(E\)本の割合で電気力線が面を垂直に貫く。ここで,\(Q\)[C]の正電荷を中心とする半径\(r\)[m]の球面Sを考える。この球面上における電場の強さ\(E\)[N/C]は\(\displaystyle E=k\frac{Q}{r^2}\)であるので,単位面積当たり\(\displaystyle E=k\frac{Q}{r^2}\)本の電気力線が球面Sを貫くことになる。球面Sの面積は\(4\pi r^2\)であるので,球面Sを貫く電気力線の総数を\(N\)本とすると,\(\displaystyle N=k\frac{Q}{r^2}\times4\pi r^2=4\pi kQ\)本となる。
点電荷に限らず,\(Q\)[C]の帯電体からは\(4\pi kQ\)本の電気力線が出て,負電荷\(-Q\)の帯電体には\(4\pi kQ\)本の電気力線が入る。これをガウスの法則という。
電位
電位
電位と電気力による位置エネルギー:\(U=qV\)
電気力による位置エネルギー\(U\)[J],電位\(V\)[V],電気量\(q\)[C]
重力がする仕事と同様に,静電気力がする仕事も途中の経路に関係なく,始点と終点の位置だけで決まる保存力である。\(+1\)Cの電荷が基準点まで動くときの電気力がする仕事を電位という。電位の単位は\(\rm J/C=V\)(ボルト)を用いる。電気量\(q\)[C]の電荷が電位\(V\)[V]の位置にあるとき,この電荷がもつ電気力による位置エネルギー\(U\)[J]は\(U=qV\)で表される。
電位差と仕事
\(q\)[C]の電荷が点A(電位\(V_{\rm A}\))から点B(電位\(V_{\rm B}\))まで移動するとき,静電気力がする仕事\(W_{\rm AB}\)[J]は,静電気力による位置エネルギーの差\(W_{\rm AB}=qV_{\rm A}-qV_{\rm B}=q(V_{\rm A}-V_{\rm B})\)で表される。ここで,\(V=V_{\rm A}-V_{\rm B}\)とすると,\(W_{\rm AB}=qV\)と表される。この\(V\)を2点間の電位差(または電圧)という。
電場と電位差との関係
一様な電場と電位差:\(V=Ed\)
電位差\(V\)[V],一様な電場の強さ\(E\)[V/m],距離\(d\)[m]
ここで強さと向きがいたるところで一定である電場(一様な電場)を考える。強さ\(E\)[N/C]の一様な電場の中にある電気量\(q\)[C]の正電荷が,電場の向きにそってAからBまで\(d\)[m]の距離を移動するとき,静電気力(\(F=qE\))のする仕事は\(W_{\rm AB}=qEd\)[J]と表される。一方,AB間の電位差を\(V\)とすると,\(W_{\rm AB}=qV\)[J]の式から,\(V=Ed\)が成りたつ。
点電荷のまわりの電位
点電荷のまわりの電位:\(\displaystyle V=k\frac{Q}{r}\)
電位\(V\)[V],クーロンの法則の比例定数\(k\)[N・m²/C²],点電荷の電気量\(Q\)[C]
電気量\(Q\)[C]の点電荷から距離\(r\)[m]離れた点における電位\(V\)[V]は,電位の基準の位置を無限遠にとると,\(\displaystyle V=k\frac{Q}{r}\)と表される。
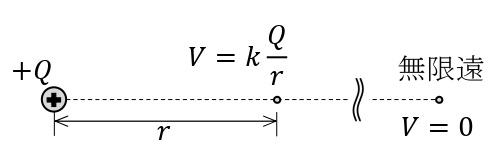
等電位面
電位が等しい点を立体的に連ねてできる面を等電位面,平面上で連ねてできる線を等電位線という。一定の電位差ごとに等電面を描くと,電場が強いほど等電位面の間隔は狭くなる。また,電気力線は等電位面(等電位線)に直行する。










コメント