本記事では、『剛体にはたらく力・モーメント』について解説していきたいと思います。
大学受験物理講師・ともくん
青森県出身。37歳。
経歴 東北大学物理学科→東北大学大学院理学研究科物理学専攻→公務員(教職ではない)→塾業界に転職。講師歴約10年(物理・数学)
歴代合格実績：旧帝大医学部、国公立大・私大医学部、東工大、旧帝大等多数
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
剛体
力を加えても変形しない理想的な物体を剛体という。剛体の運動は，2つの基本的な運動（物体全体が向きを変えずに平行に移動する並進運動とある点のまわりの回転運動）を組み合わせたものになっている。
剛体にはたらく力の移動
物体の大きさを考えたとき，同じ大きさ，向きの力を加えても，力の作用線が異なると物体に対する力の効果が変わる。逆に，剛体にはたらく力を作用線上で移動させても，その効果は変わらない。
力のモーメント
力のモーメント：\(M=r\times F\)
力のモーメント\(M\)[N・m]，力の大きさ\(F\)[N]，うでの長さ\(r\)[m]
物体の受ける力が物体を回転させるとき，この回転を起こす作用のことを，力のモーメントという。
剛体中の点Pに，力\(\overrightarrow{F}\)がはたらいている場合を考える。ある点Oまわりの力のモーメントは，点Oからこの力の作用戦までの距離（うでの長さ）\(r\)[m]と点Pにはたらく力の大きさ\(F\)[N]の積\(r\times F\)で計算できる。
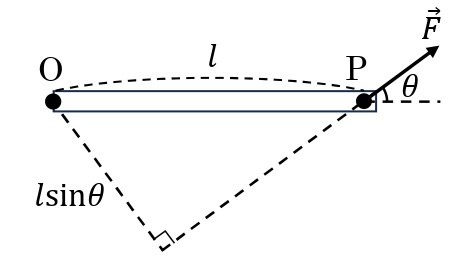
例えば下図のように，点Pに大きさ\(F\)[N]の\(\overrightarrow{F}\)がはたらく場合，Oのまわりの力のモーメン卜の大きさ\(M\)[N・m]は，OP間の距離を\(l\)[m]，OPを通る直線と\(\overrightarrow{F}\)がなす角を\(\theta\)とすると，うでの長さは\(l\sin\theta\)とあらわされるので
\begin{eqnarray}M&=&(うでの長さ)\times(力の大きさ)\\&=&l\sin\theta\times F\\&=&Fl\sin\theta\end{eqnarray}
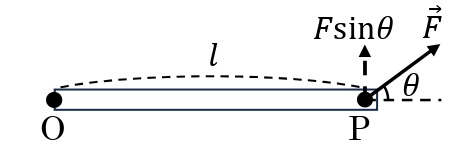
となる。一方，力のモーメン卜の大きさは
\begin{eqnarray}M&=&(\rm OP間の距離)\times(力の\rm OPに対して垂直な成分の大きさ)\\&=&l\times F\sin\theta\\&=&Fl\sin\theta\end{eqnarray}
のように解釈することもできる。
剛体のつりあいの条件
剛体に力\(\overrightarrow{F_1}\)，\(\overrightarrow{F_2}\)，\(\overrightarrow{F_3}\)，\(\cdots\)が加わっている状態で静止しているとき，この剛体はつり合っている，という。このとき\(\overrightarrow{F_1}\)のモーメン卜を\(M_1\)，\(\overrightarrow{F_2}\)のモーメン卜を\(M_2\)，\(\cdots\cdots\)とすると
並進運動しない条件：
\(\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}+\cdots=0\)
回転運動しない条件：
\(M_1+M_2+M_3\cdots=0\)
が成り立つ。
重心
質量\(m_1\)，\(m_2\)，\(m_3\)，\(\cdots\)の小物体が座標\(x_1\)，\(x_2\)，\(x_3\)，\(\cdots\)の所にあるとき，
重心：\(\displaystyle x_G=\frac{m_1x_1+m_2x_2+m_3x_3\cdots}{m_1+m_2+m_3\cdots}\)
物体を非常に多くの小さな部分に分けて考えるとき，各部分にはたらく重力の合力の作用点を重心という。重心に対する力のモーメントの総和は0となる。したがって，剛体の重心を支えると，バランスをとることができる。
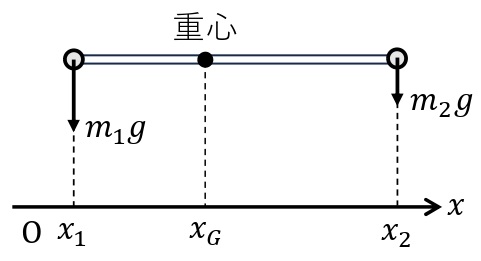
下図のように，軽い棒で結ばれた小物体1，小物体2の重心を考える。小物体1，小物体2の質量を\(m_1\)[kg]，\(m_2\)[kg]，位置を\(x_1\)，\(x_2\)，重心の位置を\(x_G\)とする。反時計回りを正とし，重心に対する力のモーメントのつりあいを考えると，
\begin{eqnarray}\displaystyle m_1g(x_G-x_1)&-&m_2g(x_2-x_G)=0\\(m_1+m_2)x_G&=&m_1x_1+m_2x_2\\x_G&=&\frac{m_1x_1+m_2x_2}{m_1+m_2}&\end{eqnarray}
\(xy\)平面上にある2物体の重心の座標を求めるときは，\(x\)座標，\(y\)座標ごとに同様な計算をすればよい。また，複数個の小物体についても，上式の操作をくり返せば求めることができるので，重心の座標\((x_G，y_G)\)は次の式で表すことができる。
\begin{eqnarray}\displaystyle x_G&=&\frac{m_1x_1+m_2x_2+m_3x_3+\cdots}{m_1+m_2+m_3+\cdots}\end{eqnarray}
\begin{eqnarray}\displaystyle y_G&=&\frac{m_1y_1+m_2y_2+m_3y_3+\cdots}{m_1+m_2+m_3+\cdots}\end{eqnarray}
コメント