本記事では、『コンデンサー~電気容量・コンデンサーの接続・コンデンサーに蓄えられるエネルギー~』について解説していきたいと思います。

予備校講師ともくん
専門科目:物理
経歴:東北大学物理学科
→東北大学大学院理学研究科物理学専攻
→公務員(教職ではない)
→塾業界に転職
→予備校&塾に出講中のプロ講師
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
コンデンサー
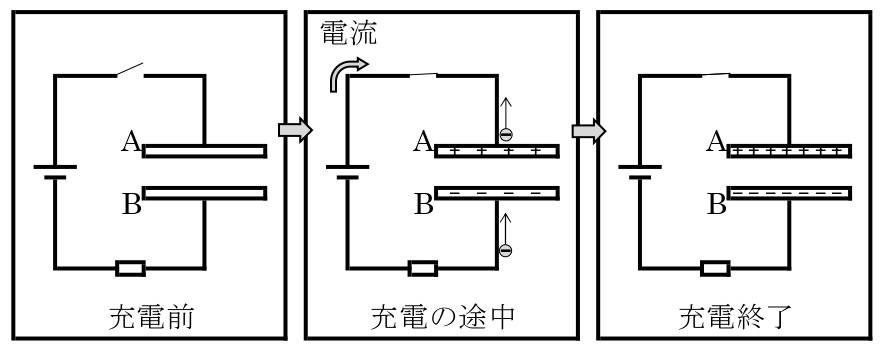
帯電していない2枚の金属板を向かいあわせ,電源に導線で繋ぐと,自由電子が極板Aから極板Bに向かって移動する。電荷の移動に伴って,極板間の電位差も大きくなる。極板間の電位差が電池の電圧と等しくなると自由電子の移動が止まる。その後,スイッチを開いても,金属板上にある電荷はクーロン力により互いに引き合うので,極板の電荷は失われない。このように電荷を蓄えることができる,このような装置をコンデンサーという。
コンデンサーの電気容量
コンデンサーの電気容量
コンデンサー:\(Q=CV\)
コンデンサーの電気量\(Q\)[C],コンデンサーの電気容量\(C\)[F],極板間の電位差\(V\)[V]
コンデンサーの極板に蓄えられるに蓄えられる電気量をそれぞれ\(+Q\),\(-Q\)とすると,\(Q\)は極板間の電位差\(V\)に比例する。よって\(Q=CV\)が成り立つ。ここで,比例定数\(C\)はコンデンサーの電気容量という。\(C\)の単位はファラド(記号F)と定める。
平行板コンデンサーの電場
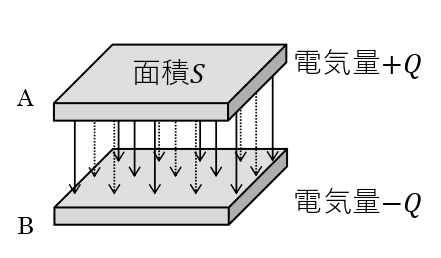
同じ大きさで同じ形の2枚の平らな金属板を向かい合わせたコンデンサーを平行板コンデンサーという。平行板コンデンサーの極板間には,2つの極板の電荷によって,一様な電場が生じている。ここで,下図のように極板A,Bの電気量をそれぞれ\(+Q\),\(-Q\)[C],極板の片面の面積を\(S\)[m²]とする。極板Aからは極板の両側に\(2\pi k_0Q\)本ずつ電気力線が出ている。また,極板Bは極板の両側から\(2\pi k_0Q\)本ずつ入ってきている。よって,極板A,B間には合わせて\(4\pi k_0Q\)本の電気力線が極板AからBへ向かっている。極板間の電場の強さ\(E\)は,単位面積当たりを垂直に貫く電気力線の数なので,\(\displaystyle E=\frac{4\pi k_0Q}{S}\)が求められる。
平行板コンデンサーの電気容量
極板間の電位差\(V\)[V]は,極板間の間隔を\(d\)[m]とすると,\(\displaystyle V=Ed=\frac{4\pi k_0Q}{S}d\)が成り立つ。これを,\(Q\)について解くと,\(\displaystyle Q=\frac{1}{4\pi k_0}\cdot\frac{S}{d}V\)となる。これより,\(Q=CV\)と比較すると,コンデンサーの電気容量\(C\)は,次の式で表される。
\begin{eqnarray} \displaystyle C=\frac{1}{4\pi k_0}\cdot\frac{S}{d}=\varepsilon_0\frac{S}{d} \end{eqnarray}
ここで,\(\displaystyle \varepsilon_0=\frac{1}{4\pi k_0}\)は真空の誘電率と呼ばれる定数で,\(\varepsilon_0≒8.85\times10^{-12}\)F/mである。
コンデンサーと誘電体
コンデンサーの電気容量:\(\displaystyle C=\varepsilon\frac{S}{d}\)
コンデンサーの電気容量\(C\)[F],誘電率\(\varepsilon\)[F/m],極板の面積\(S\)[m²],極板の間隔\(d\)[m]}
平行板コンデンサーを充電した後に,スイッチを切った状態で極板間に誘電体を入れる。誘電分極により,極板と接する誘電体の表面に極板と反対の符号の電荷が現れることにより,極板間の電位差\(V\)が小さくなり,コンデンサーの電気容量\(C\)の値は増大する。
極板間が真空の場合の電気容量\(C_0\)の平行板コンデンサーに誘電体を隙間なく挿入して,電気容量が\(C\)となったとき,その倍率\(\displaystyle\varepsilon_r=\frac{C}{C_0}\)を,誘電体の比誘電率という。ここで,\(\varepsilon=\varepsilon_r\varepsilon_0\)とおくと,コンデンサーの電気容量は\(\displaystyle
C=\varepsilon_rC_0=\varepsilon_r\varepsilon_0\dfrac{S}{d}=\varepsilon\dfrac{S}{d}\)で表される。ここで,\(\varepsilon\)を誘電体の誘電率という。
コンデンサーの接続
コンデンサーの合成容量
並列接続:\(C=C_1+C_2\)
並列接続:\(\displaystyle\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}\)
合成容量\(C\)[F],それぞれの電気容量\(C_1\),\(C_2\)[F]
並列接続
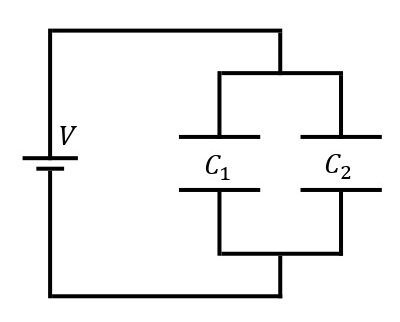
電気容量が\(C_1\),\(C_2\)[F]のコンデンサーを下図のように並列に接続し,起電力\(V\)[V]の電源を繋げる。このとき,2つのコンデンサーには電圧\(V\)がかかるので,各コンデンサーに蓄えられる電気量は,\(Q_1=C_1V\),\(Q_2=C_2V\)となる。ここで全体の電気量\(Q\)[C]は,\(Q=Q_1+Q_2=(C_1+C_2)V\)となるので,これを\(Q=CV\)と比較すると,このコンデンサーの電気容量は,\(C=C_1+C_2\)となる。これを合成容量という。
一般に,電気容量\(C_1\),\(C_2\cdots,C_n\)[F]の\(n\)個のコンデンサーを並列接続したときの合成容量\(C\)[F]は,次の式で与えられる。
\begin{eqnarray}C=C_1+C_2+\cdots+C_n\end{eqnarray}
直列接続
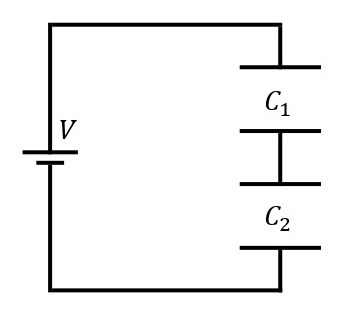
電気容量が\(C_1\),\(C_2\)[F]のコンデンサーを下図のように直列に接続し,起電力\(V\)[V]の電源を繋げる。このとき,上端,下端の極板にはそれぞれ\(+Q\),\(-Q\)[C]の電荷が蓄えられ,上,下のコンデンサーの接続部側の極板には,静電誘導によって\(-Q\),\(+Q\)[C]の電荷が現れる。すなわち,2つのコンデンサーに蓄えられる電荷はともに\(Q\)[C]である。よって,各コンデンサーにかかる電圧を\(V_1\),\(V_2\)とすると,\(\displaystyle V_1=\frac{Q}{C_1}\),\(\displaystyle V_2=\frac{Q}{C_2}\)となる。ここで接続したコンデンサーの両端の電位差\(V\)[V]は,\(\displaystyle V=V_1+V_2=\left(\frac{1}{C_1}+\frac{1}{C_2}\right)Q\)となるので,このコンデンサーの電気容量\(C\)は,\(\displaystyle\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}\)となる。
一般に,電気容量\(C_1\),\(C_2\cdots,C_n\)[F]の\(n\)個のコンデンサーを直列接続したときの合成容量\(C\)[F]は,次の式で与えられる。
\begin{eqnarray}\displaystyle\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\cdots\frac{1}{C_n}\end{eqnarray}
コンデンサーに蓄えられるエネルギー
コンデンサーに蓄えられる静電エネルギー:\(\displaystyle U=\frac{1}{2}QV=\frac{1}{2}CV^2=\frac{Q^2}{2C}\)
コンデンサーに蓄えられる静電エネルギー\(U\)[J],コンデンサーの電気量\(Q\)[C],極板間の電位差\(V\)[V],コンデンサーの電気容量\(C\)[F]
電気容量\(C\)[F]のコンデンサーを電圧\(V\)[V]の電池につないで充電する。極板間の電位差が\(V\)[V]になると,コンデンサーに電気量\(Q=CV\)[C]の電荷が蓄えられ,充電が完了する。このとき,コンデンサーの静電エネルギーは,次のように表される。
\begin{eqnarray}\displaystyle U=\frac{1}{2}QV=\frac{1}{2}CV^2=\frac{Q^2}{2C}\end{eqnarray}
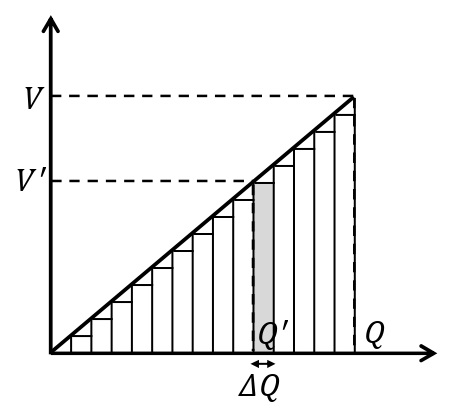
電気量\(Q’\)のとき極板間の電圧は\(\displaystyle V’=\frac{Q’}{C}\)であるので,電圧\(V’\)と電気量\(Q’\)の関係は下図のようになる。このとき,小さな電気量\(\it\Delta Q\)[C]を移動させるのに必要な仕事は,この間の電位差がほぼ一定であるとみなして,\(\it\Delta Q\times V’\)[J]であるから。これは,灰色の長方形の面積で表される。電位差\(V\)[V]まで充電する仕事\(W\)[J]は,これらの長方形の面積の総和になる。よって,\(\it\Delta Q\)をきわめて小さくとるとこれは\(\Delta\rm OAB\)の面積になるからこの仕事は\(\displaystyle W=\frac{1}{2}QV\)[J]になる。










コメント