本記事では、『電磁誘導～レンツの法則・ファラデーの電磁誘導の法則・磁場中を運動する導体棒・誘導起電力とエネルギー』について解説していきたいと思います。
大学受験物理講師・ともくん
青森県出身。37歳。
経歴 東北大学物理学科→東北大学大学院理学研究科物理学専攻→公務員(教職ではない)→塾業界に転職。講師歴約10年(物理・数学)
歴代合格実績：旧帝大医学部、国公立大・私大医学部、東工大、旧帝大等多数
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
電磁誘導の法則
電磁誘導
棒磁石を動かすなどで，コイル内部の磁場の変化するとコイルに電圧が生じる。これを電磁誘導という。電磁誘導によって生じた起電力を誘導起電力，誘導起電力によって，閉じた回路に流れる電流を誘導電流という。
磁束
面積\(S\)[m²]の平面領域を一様な磁束密度\(B\)[T]の磁場が垂直に貫く場合，磁束密度と面積の積\(\it\Phi=BS\)を，平面領域を貫く磁束という。磁束の単位には磁気量と同じ単位Wbを用いる。
レンツの法則
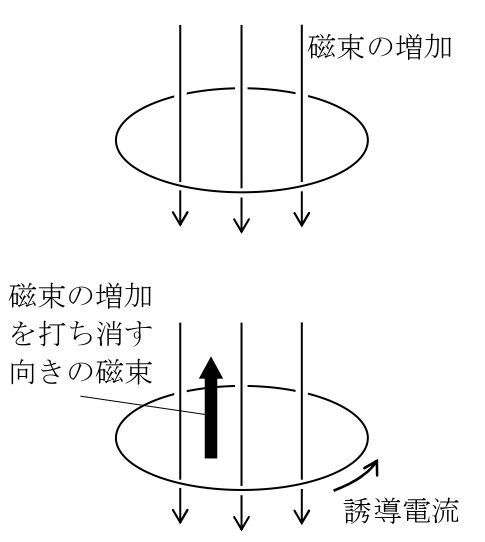
誘導電流がつくる磁場の向きは，コイルを貫く磁束が増えるときは磁束を減らそうとする向き，磁束が減るときは磁束を増やそうとする向きとなる。このように，誘導起電力はそれによって流れる誘導電流のつくる磁束が，外から加えられた磁束の変化を打ち消すような向きに生じる。これをレンツの法則という。
図のように円形の導線に垂直に磁場がかかっていうる場合を考える。磁場が増加すると導線を囲む領域を貫く磁束が増加する。ここで，円形の導線に誘導電流が流れ，増加した磁束を打ち消すような磁場が発生させることになる。
ファラデーの電磁誘導の法則
ファラデーの電磁誘導の法則：\(\displaystyle V=-N\frac{\it\Delta\Phi}{\it\Delta t}\)
誘導起電力\(V\)[V]，コイルの巻き数\(N\)，磁束の変化\(\it\Delta \Phi\)[Wb]，時間\(\Delta t\)[s]
コイルを貫く磁束が\(\it\Delta t\)[s]の間に\(\it\Delta\Phi\)だけ変化するとき，コイルに生じる誘導起電力\(V\)[V]の大きさは，コイルを貫く磁束の時間変化率\(\displaystyle\frac{\it\Delta\Phi}{\Delta t}\)に比例する。これをファラデーの電磁誘導の法則という。
1巻きコイルに生じる誘導起電力$V$[V]は次の式で表される。
\begin{eqnarray}\displaystyle V=-\frac{\it\Delta\Phi}{\it\Delta t} \end{eqnarray}
この式の負の記号は，磁束の変化を打ち消す向きに誘導起電力が生じること(レンツの法則)を表している。コイルが\(N\)回巻きのときは1巻きのコイルを\(N\)個つながっていると考えることができるので，誘導起電力が\(N\)倍になり，次の式で表すことができる。
\begin{eqnarray}\displaystyle V=-N\frac{\it\Delta\Phi}{\it\Delta t} \end{eqnarray}
磁場中を運動する導体棒
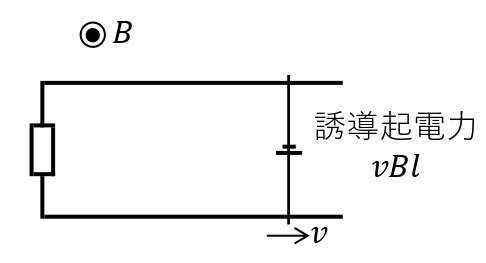
図のような回路を考える。磁束密度が\(B\)[T]の一様な磁場の中で，長さ\(l\)[m]の導体棒を磁場と垂直な方向に\(v\)[m/s]で動かす。導体棒は時間\(\it\Delta t\)[s]の間に\(v\it\Delta t\)[m]だけ移動することになる。このとき，回路が囲む領域の面積は\(\it\Delta S=lv\it\Delta t\)[m²]だけ変化するので，回路を貫く磁束は\(\it\Delta \Phi=B\it\Delta S=Blv\it\Delta t\)[Wb]だけ増加する。よって導体棒に生じる誘導起電力の大きさ\(V\)[V]はファラデーの電磁誘導法則より，
\begin{eqnarray}\displaystyle V&=\left|-\frac{\it\Delta\Phi}{\it\Delta t}\right|\\ &=\frac{Blv\it\Delta t}{\it\Delta t}\\ &=vBl \end{eqnarray}
と表すことができる。
ローレンツ力と誘導起電力
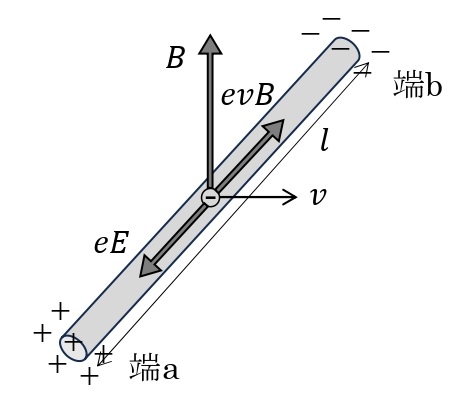
時間的に変化しない磁場中を導体が動く場合の誘導起電力は，ローレンツ力によっても説明することができる。図のように，長さ\(l\)[m]の導体棒が磁束密度\(B\)[T]の磁場中に対して垂直に速さ\(v\)[m/s]で移動しているとする。このとき，導体棒中の自由電子（電気量\(-e\)[C]）は棒とともに速さ\(v\)で動いているので，導体棒の端a→端bの向きにローレンツ力\(evB\)[N]を受ける。その結果，導体棒の端bは負に，端aは正に帯電し，導体棒内に端a→端bに向かって電場ができる。導体内の電場の大きさを\(E\)[V/m]とすると，電子はこの電場から導体棒の端b→端aの向きに静電気力\(eE\)[N]を受ける。やがて，静電気力とローレンツ力がつり合うまで電子は移動する。このとき，つり合いの式より\(eE=evB\)が成り立つので，\(E=vB\)と表すことができる。よって，導体棒の端aから端bまでの電位差\(V\)[V]は，次の式で表される。
\begin{eqnarray}\displaystyle V=El=vBl\end{eqnarray}
これが，磁場を横切る導線の両端に生じる誘導起電力である。
誘導起電力とエネルギー
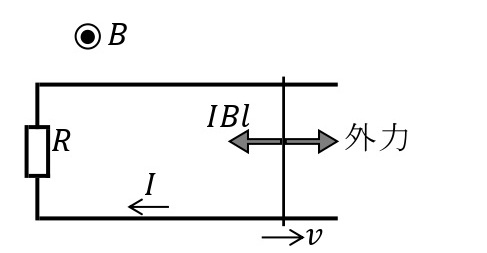
図のような回路を考える。磁束密度が\(B\)[T]の一様な磁場の中で，長さ\(l\)[m]の導体棒を磁場と垂直な方向に外力を加えて一定の速さ\(v\)[m/s]で動かすと，導体棒に\(vBl\)[V]の誘電起電力が生じる。回路につながれた抵抗の抵抗値を\(R\)[Ω]とすると，回路には\(\displaystyle I=\frac{vBl}{R}\)[A]の電流が流れるので，抵抗で消費される電力は\(\displaystyle P=I^2R=\frac{(vBl)^2}{R}\)と求めることができる。一方，導体棒には磁界から運動を妨げる方向に大きさ\(IBl\)[N]の力がはたらく。導体棒を一定の速さ動かし続けるためには，この力と同じ大きさの外力\(F=IBl\)[N]を導体棒に加え続ける必要がある。よって，導体棒に摩擦がない場合，外力\(F\)がする仕事率は\(\displaystyle Fv=IBlv=\frac{(vBl)^2}{R}\)となる。
以上から，抵抗で単位時間あたりに発生するジュール熱は，外力\(F\)のする仕事率と等しい。このように，電磁誘導によって力学的な仕事が電気エネルギーに変換される場合でも，エネルギー保存則は成り立っている。
コメント