本記事では、『コイルを含む回路～自己誘導・コイルに蓄えられるエネルギー・相互誘導～』について解説していきたいと思います。
大学受験物理講師・ともくん
青森県出身。37歳。
経歴 東北大学物理学科→東北大学大学院理学研究科物理学専攻→公務員(教職ではない)→塾業界に転職。講師歴約10年(物理・数学)
歴代合格実績：旧帝大医学部、国公立大・私大医学部、東工大、旧帝大等多数
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
自己誘導
自己誘導：\(\displaystyle V=-L\frac{\it\Delta I}{\it\Delta t}\)
誘導起電力\(V\)[V]，自己インダクタンス\(L\)[H]，電流の変化\(\it\Delta I\)[A]，時間\(\Delta t\)[s]
コイルに流れる電流が変化すると，コイルの内部に生じていた磁場が変化するため，電磁誘導によって誘導起電力が生じる。これを自己誘導という。
コイルに流れる電流が\(\it\Delta t\)[s]の間に\(\it\Delta I\)[A]だけ変化すると，コイルは電流の変化を妨げる方向に\(\displaystyle V=-L\frac{\it\Delta I}{\it\Delta t}\)[V]の誘導起電力が生じる。ここで，比例定数\(L\)はコイルの自己誘導の大きさを表し，自己インダクタンスと呼ぶ。自己インダクタンスの単位にはへンリー(記号H)を用いる。
下図のように，起電力\(V\)[V]の電池，スイッチ，コイル及び抵抗をつないだ直列回路を考える。キルヒホッフの法則より，
\begin{eqnarray}\displaystyle V-L\frac{\it\Delta I}{\it\Delta t}=IR\cdots\cdots\cdots①\end{eqnarray}
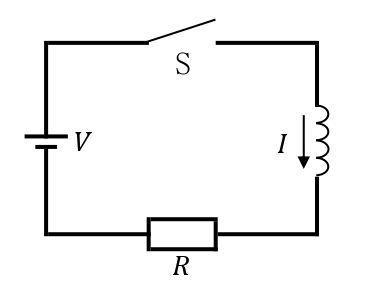
- スイッチを入れた直後
-
コイルには電流を一定に保とうとする性質がある。よって，スイッチを入れた直後はコイルに流れる電流はスイッチを入れる直前と等しく\(I=0\)となる。①式より，\(\displaystyle\frac{\it\Delta I}{\it\Delta t}=\frac{V}{L}\)が成り立つ。ここで，\(\displaystyle\frac{\it\Delta I}{\it\Delta t}\)は\(I\)-\(t\)グラフの傾きを表す。
- スイッチを入れて十分時間が経過したとき
-
スイッチを入れるとコイルに流れる電流はしだいに増加するが，十分時間が経過すると増加しなくなるので，\(\displaystyle\frac{\it\Delta I}{\it\Delta t}=\rm 0\)となる。よって，①より，\(\displaystyle I=\frac{V}{R}\)が成り立つ。
以上より，スイッチを入れた時間を\(t=0\)[s]としたときの\(I\)-\(t\)グラフは以下のようになる。
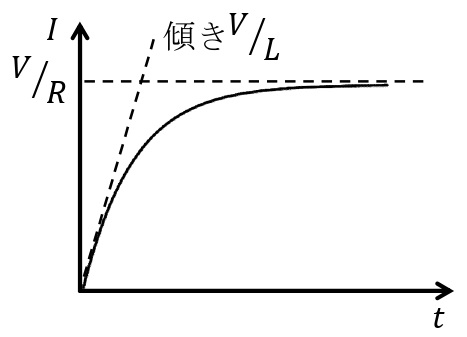
コイルに蓄えられるエネルギー
コイルに蓄えられるエネルギー：\(\displaystyle U=\frac{1}{2}LI^2\)
コイルに蓄えられているエネルギー\(U\)[J]，自己インダクタンス\(L\)[H]，電流\(I\)[A]
自己インダクタンス\(L\)[H]のコイルに流れる電流が\(I\)[A]であるとき，コイルに蓄えられているエネルギーは\(\displaystyle U=\frac{1}{2}LI^2\)[J]と表される。
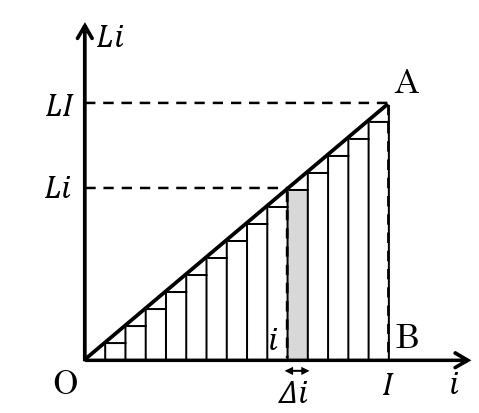
自己インダクタンス\(L\)[H]のコイルに流れる電流が時間\(\it\Delta t\)[s]で\(i\)[A]から\(i+\it\Delta i\)[A]に変化するとき，\(\displaystyle V=-L\frac{\it\Delta i}{\it\Delta t}\)の誘導起電力が発生する。この誘導起電力に逆らって，電流\(i\)を\(\it\Delta t\)の間流すときの仕事\(w\)[J]は\(\displaystyle w=i\cdot L\frac{\it\Delta i}{\it\Delta t}\it\Delta t=Li\it\Delta i\)となる。ここで，下図のようなグラフを考えると\(Li\it\Delta i\)は灰色の長方形の面積で表される。したがって，電流を\(\rm O\)から\(I\)にするときの仕事\(W\)[J]は，これらの長方形の面積の総和になる。よって\(\it\Delta i\)をきわめて小さくとると\(\Delta \rm OAB\)の面積と等しくなるので，\(\displaystyle W=\frac{1}{2}\times I\times LI=\frac{1}{2}LI^2\)と表される。これが，コイルに蓄えられるエネルギー\(U\)[J]となる。
相互誘導
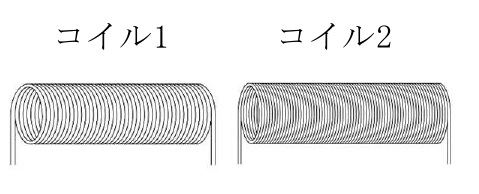
下図のように2つのコイルを並べて配置する。コイル1に流れる電流を変化させると誘導起電力が生じる。このとき，コイル2を貫く磁束も変化するため，コイル2にも誘導起電力が生じる。これを相互誘導という。
コイル1を流れる電流\(I_1\)の時間変化率を\(\displaystyle\frac{\it\Delta I_{\rm1}}{\it\Delta t}\)とするとき，コイル2に生じる誘導起電力\(V_2\)は，\(\displaystyle V_2=-M\frac{\it\Delta I_{\rm1}}{\it\Delta t}\)と表される。ここで，比例定数\(M\)を相互インダクタンスといい，その値は2つのコイルの巻数や位置等で決まる。相互インダクタンスの単位は，自己インダクタンス\(L\)の単位と同じH(ヘンリー)である。
コメント