【高校物理の要点】電子と光（1）～真空放電・ミリカンの実験・光量子仮説・光電効果

本記事では、『電子と光（1）～真空放電・ミリカンの実験・光量子仮説・光電効果』について解説していきたいと思います。

電子の電荷と質量

真空放電

低圧のガラス管内で高電圧をかけて放電させると，管全体が気体特有の色の光を発するようになる。このような低圧の気体による放電を真空放電という。さらに気体の圧力を下げると，管内の光は消え，陽極側の周りのガラス管が蛍光を発する。これは陰極から出た何かが陽極側に向かって進み，管壁にぶつかることによって起こると考えられた。この陰極から出ているものを陰極線という。その後の様々な実験により，陰極線に次のような性質があることがわかった。

• 直進する。
• 陰極線のあたった物体は，蛍光を発したり，温度が上昇したりする。
• 電場や磁場によって，軌道が変化する。

以上から，陰極線は負の電荷をもつ粒子の流れであると考えられるようになった。こうして電子が発見され，陰極線が電子線であることがわかった。電子の電気量と質量を決めるために，トムソンは，電場及び磁場をかけたときの陰極線のふるまいを調べることによって，陰極線の質量\(m\)[kg]に対する電荷の大きさ\(e\)[C]の比\(\displaystyle\frac{e}{m}\)[C/kg]を測定した。実験の結果，比電荷は，陰極に用いる金属や管内の気体の種類によらず，常に一定の値\(\displaystyle\frac{e}{m}≒1.76\times10^{11}\)C/kgになることがわかった。このことから，物質の中には負電荷をもった電子が共通に含まれていることが明らかになった。

ミリカンの実験

電子の電気量を求めるために，ミリカンは2つの平行な極板をおいて，その中に霧吹きから油滴を吹きこみ，個々の油滴の運動を調べた。

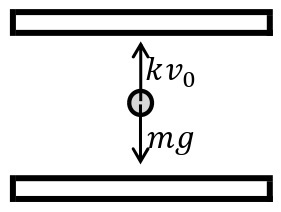
まず，極板間に電圧をかけずに，落下する油滴の速さを測定する。落下する油滴には重力のほか，速さ\(v\)[m/s]に比例する空気抵抗\(kv\)[N]がはたらく。油滴は軽いので，落下を始めてすぐに空気抵抗により終端速度\(v_0\)[m/s]に達する。油滴の質量を\(m\)[kg]とすると，力のつりあいより，

\begin{eqnarray}\displaystyle mg=kv_0 \end{eqnarray}

が成り立つ。

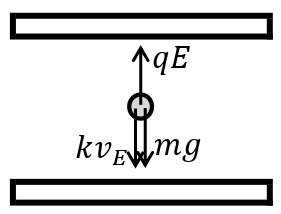
次に，平行板電極に電圧をかけ，同じ油滴を上昇させる。このときも油滴はすぐに終端速度\(v_E\)[m/s]に達する。このとき，電場の強さを\(E\)[V/m]，油滴の電気量を\(q\)[C]とすると，力のつりあいより，

\begin{eqnarray}\displaystyle qE=mg+kv_E \end{eqnarray}

が成り立つ。以上から，\(\displaystyle q=\frac{k(v_0+v_E)}{E}\)[C]として，油滴の速度\(v_0\)[m/s]，\(v_E\)[m/s]を測定することによって，油滴の電気量\(q\)[C]を求めることができる。

この実験から，得られる油滴の電気量\(q\)[C]が，すべて\(e=1.6\times10^{-19}\)Cの整数倍とみなせることが確認された。この値\(e\)[C]が電荷の最小単位で，電気素量と呼ばれる。

光の粒子性

光量子仮説

光子のエネルギー：\(\displaystyle E=h\nu=\frac{hc}{\lambda}\)

光子のエネルギー\(E\)[J]，真空中の光の速さ\(c\)[m/s]，プランク定数\(h\)[J・s]，光の波長\(\lambda\)[m]，光の振動数\(\nu\)[Hz]

アインシュタインは，光は，光子または光量子という光速で動く粒子の集まりであり，光子1個のエネルギーは振動数に比例することを提唱した。これを光量子仮説という。光量子仮説によれば，光子1個のエネルギー\(E\)[J]は，比例定数を\(h\)[J・s]，光の振動数を\(\nu\)[Hz]として，次の式で表される。

\begin{eqnarray}\displaystyle E=h\nu=\frac{hc}{\lambda} \end{eqnarray}

また，この比例定数を\(h=6.63\times10^{-34}\)J・sをプランク定数という。

光電効果

光電効果：\(K_0=h\nu-W\)

電子の運動エネルギーの最大値\(K_0\)[J]，プランク定数\(h\)[J・s]，光の振動数\(\nu\)[Hz]，仕事関数\(W\)[J]

物質に紫外線などの光を当てると，物質中の電子が飛び出す。この現象を光電効果という。また，光電効果が起こるときに飛び出す電子を光電子という。

下図のような実験装置を用いて光電効果を調べた。

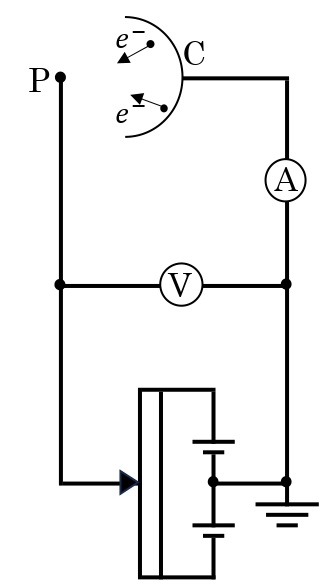
光電管の陰極Cに光源Sから光を当てると，光電子が飛び出し，電極Pに到達することで電極間に電流(光電流)が流れる。電極間の電圧，光の強さ，振動数を変えて，光電流の変化を測定したところ，次のような特徴があることがわかった。

• 光電効果が起こるためには，光の振動数がある値\(\nu_0\)[Hz]より大きい必要がある。この\(\nu_0\)[Hz]は金属の種類によって決まり，限界振動数という。
• 光の振動数が\(\nu_0\)[Hz]より大きい場合，光を当てるとただちに光電効果が起こる。
• 光の振動数が一定のとき，光電流の強さは光の強さに比例する。
• 光電子の運動エネルギーの最大値\(K_0\)[J]は光の振動数が大きいほど大きくなる。

光電子の運動エネルギーの最大値\(K_0\)[J]は光電流が流れなくなるときの陽極Pの電位の絶対値\(V_0\)[V]から求めることができる。このとき，\(K_0=eV_0\)が成り立ち，この\(V_0\)[V]を阻止電圧と呼ばれる。

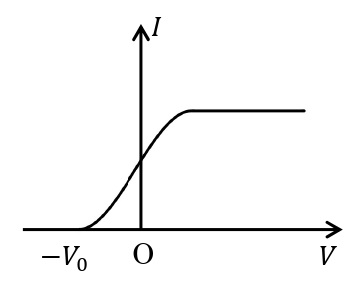
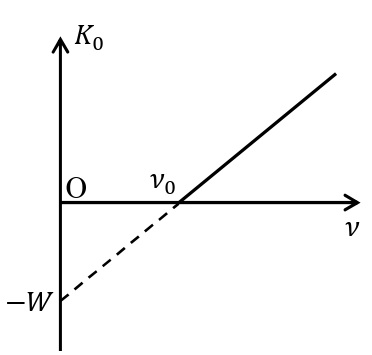
\(\nu(≧\nu_0)\)[Hz]と\(K_0\)[J]の関係をグラフに描くと下図のような直線になる。このことから，

\begin{eqnarray}\displaystyle K_0=h\nu-W \end{eqnarray}

という関係式で表すことができる。ここで\(W\)は陰極Cの種類によって決まる定数で，仕事関数と呼ばれる。限界振動数\(\nu_0\)[Hz]では，\(K_0=0\)[J]であるので，\(W=h\nu_0\)[J]で表される。

電子ボルト

仕事関数や電子，光子1個のエネルギーは極めて小さい。このような場合，エネルギー単位として電子ボルト(eV)が用いられる。1eVは真空中で1個の電子が1Vの電圧によって加速されるときに得られる運動エネルギーの大きさに等しく，次のような関係が成り立つ。

\begin{eqnarray}\displaystyle 1\rm{eV}=(1.60\times10^{-19}C)\times1\rm{V}=1.60\times10^{-19}J \end{eqnarray}