本記事では、『原子核(1)~ラザフォードの原子模型・水素原子のスペクトル・ボーアの理論とエネルギー準位』について解説していきたいと思います。

予備校講師ともくん
専門科目:物理
経歴:東北大学物理学科
→東北大学大学院理学研究科物理学専攻
→公務員(教職ではない)
→塾業界に転職
→予備校&塾に出講中のプロ講師
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
ラザフォードの原子模型
ラザフォードらは,原子の構造を調べるために,ラジウムから出る\(\alpha\)粒子(電気量\(+2e\))を薄い金箔に当て,その散乱の様子を調べた。その結果,ほとんどの\(\alpha\)粒子は素通りするが,中には大きく進路を曲げられて散乱するものがあることがわかった(ラザフォード散乱)。ラザフォードはこのような大きな散乱が起こるのは,質量の大きな正電荷が原子内のごく小さな領域に集中しており,この付近を通過する\(\alpha\)粒子が正電荷から強い斥力を受けるためであると考えた。この正電荷は原子核と名づけられ,ラザフォードによって,次のような原子模型が提唱された。
- 原子の中心には,体積が小さく重い原子核がある。原子番号\(Z\)の原子は,電気素量の\(Z\)倍の正電荷をもつ原子核と,それをとりまく\(Z\)個の電子からなる。
- 電子は,原子核との間にはたらく静電気力によって,原子核の周りを円運動している。
これを,ラザフォードの原子模型という。
水素原子のスペクトル
光を波長によって分けたものをスペクトルという。一般に,高温の固体や液体が出す光は,さまざまな波長の光が連続的に分布した連続スペクトルを示す。一方,高温の気体が出す光は,いくつかの輝いた線がとびとびに分布する線スペクトルを示す。線スペクトルは,気体の原子が発する光で,その波長は原子の種類によって決まっている。
水素原子は,原子核のまわりを1個の電子がまわっている最も簡単な構造をしている。バルマーは,水素のスペクトルは,可視光線領域の光の波長\(\lambda\)[m]が,\(\displaystyle\lambda=3.65\times10^{-7}\times\frac{n^2}{n^2-2^2}\) (\(n=3,4,5,6\))で表されることを発見した。このスペクトルを,バルマー系列いう。
その後,紫外線領域にあるライマン系列,赤外線領域にあるパッシェン系列にも同様な規則性が成り立つことが発見された。これらすべての系列は,次の形に表される。
\begin{eqnarray}\displaystyle\frac{1}{\lambda}=R\left(\frac{1}{n^2}-\frac{1}{m^2}\right) \end{eqnarray}
ここで,\(n\),\(m\)は自然数で\(n<m\)である。また,\(R\)は\(R≒1.10\times10^7\)/mなる定数で,リュードベリ定数という。この式で\(n=1\)の場合がライマン系列,\(n=2\)の場合がバルマ一系列,\(n=3\)の場合がパッシェン系列となる。
ボーアの理論
従来の電磁波の理論では,電子が原子核のまわりを円運動すると,電磁波を放射してエネルギーを失う。その結果,電子の軌道半径は小さくなっていき原子核に墜落してしまう。そこで,ボーアは次のような仮説を提唱し,水素原子のスペクトルの説明に成功した。
量子条件
ボーアの量子条件:\(\displaystyle mvr=n\frac{h}{2\pi}\) \((n=1,2,3,\cdots)\)
電子の質量\(m\)[kg],電子の速さ\(v\)[m/s],電子の軌道半径\(r\)[m],プランク定数\(h\)[J・s],量子数\(n\)
原子には定常状態があり,定常状態では電磁波を出さずに安定して存在できる。定常状態の条件は,電子の質量を\(m\)[kg],速さを\(v\)[m/s],軌道半径を\(r\)[m],プランク定数を\(h\)[J・s]とすると,
\begin{eqnarray}\displaystyle mvr=n\frac{h}{2\pi} (n=1,2,3,\cdots) \end{eqnarray}
の条件を満たす。この式は,のちにド・ブロイが提唱した物質波の考え\(\displaystyle\lambda=\frac{h}{mv}\)を用いて書き直すと,
\begin{eqnarray}\displaystyle 2\pi r=n\frac{h}{mv}=n\lambda (n=1,2,3,\cdots) \end{eqnarray}
となる。これは,軌道の1周の長さが電子波の波長の整数倍になるとき定常状態になることを表している。
量子条件における自然数\(n\)を量子数という。量子数\(n\)に対応する軌道半径を\(r_n\)とすると,\(r_n\)がとびとびの値となることから定常状態での電子のエネルギー\(E_n\)[J]もとびとびの値になる。このエネルギ―\(E_n\)[J]をエネルギー準位という。
振動数条件
ボーアの振動数条件:\(\displaystyle h\nu=E_n-E_{n’}\) \((n=1,2,3,\cdots)\)
プランク定数\(h\)[J・s],光の振動数\(\nu\)[Hz],エネルギー準位\(E_n\),\(E_{n’}\)
電子がエネルギー準位\(E_n\)[J]からそれよりも低いエネルギー準位\(E_{n’}\)[J]に移るとき,これらの差のエネルギーをもつ光子として放出する。また,低いエネルギー準位\(E_{n’}\)[J]にある電子は,その差と等しいエネルギーをもつ1個の光子を吸収すると高いエネルギー準位\(E_n\)[J]に移る。
すなわち,放出・吸収される光子の振動数を\(\nu\)[Hz],プランク定数を\(h\)[J・s]とすると,エネルギー準位\(E_{n}\)[J],\(E_{n’}\)[J]と光子のエネルギー\(h\nu\)との間には,
\begin{eqnarray} h\nu=E_n-E_{n’} \end{eqnarray}
の関係が成り立つ。この関係を,振動数条件という。
定常状態でのエネルギー準位
定常状態の電子の円軌道の半径
ボーアは,この2つの仮定(量子条件と振動数条件)を用いて,水素スペクトルを次のように説明した。
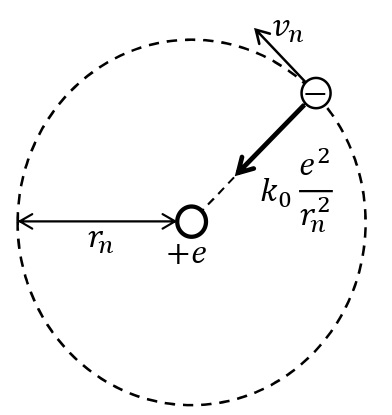
質量\(m\)[kg],電気量\(-e\)[C]の電子が,電気量\(e\)[C]の原子核のまわりを速さ\(v_n\)[m/s],半径\(r_n\)[m]で\(n\)番目の定常状態の軌道上を等速円運動している。このとき,静電気力が向心力のはたらきをするので,半径方向の運動方程式は,真空中のクーロンの法則の比例定数\(k_0\)[N・m²/C²]を用いて,
\begin{eqnarray}\displaystyle m\frac{{v_n}^2}{r_n}=k_0\frac{e^2}{{r_n}^2} (n=1,2,3,\cdots) \end{eqnarray}
と表される。ここで,量子条件の式を用いて\(v_n\)を消去すると,
\begin{eqnarray}\displaystyle r_n=\left(\frac{h}{2\pi}\right)^2\frac{n^2}{k_0me^2} (n=1,2,3,\cdots) \end{eqnarray}
となる。\(n=1\)のときの電子の軌道半径\(r_1\)をボーア半径という。
定常状態の電子のエネルギー
無限遠を基準にとると,電子の電気力による位置エネルギー\(U\)は,\(\displaystyle U=-k_0\frac{e^2}{r_n}\)と表される。したがって,\(n\)番目の定常状態の電子のエネルギー(運動エネルギーと電気力による位置エネルギーの和)\(E_n\)は,
\begin{eqnarray}\displaystyle E_n=\frac{1}{2}mv^2-k_0\frac{e^2}{r_n}=-k_0\frac{e^2}{2r_n} \end{eqnarray}
となる。この式に\(\displaystyle r_n=\left(\frac{h}{2\pi}\right)^2\frac{n^2}{k_0me^2}\)を代入すると,
\begin{eqnarray}\displaystyle E_n=-\frac{2\pi^2{k_0}^2me^4}{h^2}\cdot\frac{1}{n^2} (n=1,2,3,\cdots) \end{eqnarray}
が得られる。電子が最も原子核に近い状態(\(n=1\))にあるときが最低のエネルギー準位で,このエネルギー準位の状態を水素原子の基底状態という。\(n=2,3,\cdots\)となるにつれて,電子の軌道は原子核から離れ,エネルギーは大きくなる。これらの状態を励起状態という。
水素原子のスペクトルの説明
電子が定常状態\(E_n\)から\(E_{n’}\)へ移るときに放出される光の波長を\(\lambda\)[m]とすると,振動数条件から,
\begin{eqnarray}\displaystyle h\nu=\frac{hc}{\lambda}&=&E_n-E_{n’}\\ \frac{1}{\lambda}&=&\frac{E_n-E_{n’}}{hc}\\ &=&\frac{2\pi^2{k_0}^2me^4}{ch^3}\left(\frac{1}{n’^2}-\frac{1}{n^2}\right)\\ &=&R\left(\frac{1}{n’^2}-\frac{1}{n^2}\right) \end{eqnarray}
が導かれる。ここで,実験によって得られた水素原子の輝線の波長の式と比較すると,リュードベリ定数\(R\)は,\(\displaystyle R=\frac{2\pi^2{k_0}^2me^4}{ch^3}=1.10\times10^7\)/mと書き表せる。この式はすでにわかっていたリュードベリ定数の値と驚くほどの制度で一致した。このようにして,ボーアは,水素原子のスペクトルを理論的に説明することに成功した。










コメント