本記事では、『さなざまな力』について解説していきたいと思います。
大学受験物理講師・ともくん
青森県出身。37歳。
経歴 東北大学物理学科→東北大学大学院理学研究科物理学専攻→公務員(教職ではない)→塾業界に転職。講師歴約10年(物理・数学)
歴代合格実績：旧帝大医学部、国公立大・私大医学部、東工大、旧帝大等多数
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
物体を変形させたり，物体の運動の状態を変えたりする原因となるものを力とよぶ。物体に対して力を及ぼす点を作用点，作用点を通り力の向きに引いた直線を力の作用線という。力の効果を決める「力の大きさ・力の向き・作用点」を力の三要素と呼ぶ。
重力
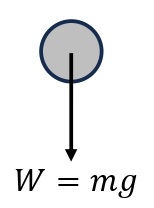
重力：\(W=mg\)
重力の大きさ\(W\)[N]，質量\(m\)[kg]，重力加速度\(g\)[m/s²]
地表近くにある物体（質量\(m\)[kg]）には，鉛直下向きに重力がはたらく。重力の大きさは重力加速度\(g\)[m/s²]を用いて\(mg\)[N]とあらわす。
ばねの弾性力
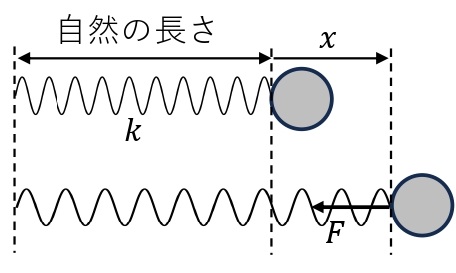
フックの法則：\(F=kx\)
弾性力の大きさ\(F\)[N]，ばね定数\(k\)[N/m]，ばねの伸び(または縮み)\(x\)[m]
ばねに力を加えるとばねは伸縮し，もとの長さ（自然長）に戻ろうとする。このように，力が加わって変形した物体が，もとの形状に戻ろうとする力を弾性力という。ばねの弾性力の大きさは伸び（または縮み）の大きさに比例する。 これをフックの法則といい，ばねに加えた力を\(F\)[N]，自然長からのばねの伸び(縮み)を\(x\)[m]とすると，\(F=kx\)が成り立つ。ここで，比例定数\(k\)[N/m]はばねによって定まる定数でばね定数という。
糸の張力
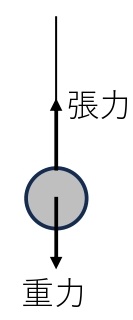
おもりに糸をつけてつるし，静止させたとき，糸はおもりに対して上向きに力を及ぼしている。このような力を，糸の張力という。質量の無視できる糸では糸の張力はどこでも同じである。
抗力
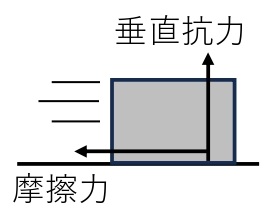
物体が他の物体と面で接触しているとき，物体が面から受ける力を抗力という。抗力のうち，接触面に対して垂直な方向にはたらく力を垂直抗力，接触面に平行な方向にはたらく力を摩擦力という。
垂直抗力
物体を机の上に置いたとき，物体は落下せず静止する。これは，机の面が物体に対して，重力と同じ大きさで逆向きの力を及ぼしているからである。この力を垂直抗力という。
摩擦力
最大摩擦力：\(F_0=\mu N\)
最大摩擦力の大きさ\(F_0\)[N]，静止摩擦係数\(\mu\)，垂直抗力の大きさ\(N\)[N]
動摩擦力：\(F’=\mu’N\)
動摩擦力の大きさ\(F’\)[N]，動摩擦係数\(\mu’\)，垂直抗力の大きさ\(N\)[N]
物体を水平なあらい面上に置き，水平方向に力を加えると，面は物体に対し運動を妨げるような力を及ぼす。この力を摩擦力という。摩擦力には静止摩擦力と動摩擦力がある。
あらい面上に置かれた物体を，面に平行に大きさ\(f\)[N]の力で引くと，\(f\)[N]が小さい間は物体は動かない。これは静止している物体に対し動きだすのを妨げるように摩擦力がはたらくからである。これを静止摩擦力という。引く力\(f\)[N]を大きくしていくと，静止摩擦力も大きくなり，物体はいつかすべりだす。すべりだす直前の静止摩擦力を最大摩擦力という。最大摩擦力\(F_0\)[N]の大きさは垂直抗力の大きさ\(N\)[N]に比例し，
最大摩擦力：\(F_0=\mu N\)
とあらわされる。ここで，\(\mu\)は静止摩擦係数といい，接触する両物体の面の種類や状態によって定まる定数である。
一方，あらい面を運動する物体にはたらく摩擦力を動摩擦力という。動摩擦力の大きさ\(F’\)[N]は一定で，垂直抗力\(N\)[N]に比例し，
動摩擦力：\(F’=\mu’ N\)
とあらわされる。ここで，\(\mu’\)は動摩擦係数といい，接触する両物体の面の種類や状態によって定まる定数である。また，一般に，\(\mu'<\mu\)である。
抵抗力
流体(液体および気体)中を運動する物体は，運動を妨げる向きに抵抗力を受ける。抵抗力の大きさは物体の速さとともに増加する。
浮力
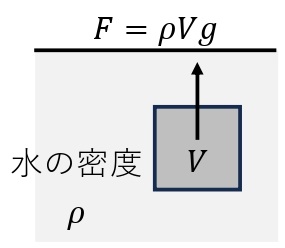
浮力：\(F=\rho Vg\)
浮力の大きさ\(F_0\)[N]，水（流体）の密度\(\rho\)[kg/m³]，物体が排除した水（流体）の体積\(V\)[m³]，重力加速度\(g\)[m/s²]}
液体と気体を合わせて流体という。流体中の物体が，まわりの流体から受ける圧力の合力を浮力という。浮力の大きさは，流体内の物体が排除した流体の重さに等しい(アルキメデスの原理)。水の密度を\(\rho\)[kg/m³]，物体が排除した水の体積を\(V\)[m³]とすると，水中の物体が受ける浮力の大さ\(F\)[N]は\(F=\rho Vg\)の式で表される。
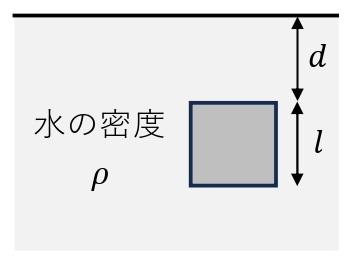
下図のように，水中にある体積\(V\)[m³]の直方体を考える。直方体の下面が水から受ける力の大きさ\(F_2\)[N]と，直方体上面が水から受ける力の大きさ\(F_1\)[N]の差は\(F=F_2-F_1\)であらわされる。大気圧を\(p_0\)[Pa]，水の密度を\(\rho\)[kg/m³]，直方体の底面積を\(S\)[m²l，直方体の高さを\(l\)[m]，上面の水深を\(d\)[m]とする。
$$F_2=\{p_0+\rho(d+l)g\}S$$
$$F_1=\left(p_0+\rho dg\right)S$$
であらわされるので，
\begin{eqnarray}F&=&F_2-F_1\\ &=&\{p_0+\rho(d+l)g\}S-\left(p_0+\rho dg\right)S\\ &=&\rho Slg\end{eqnarray}
となる。ここで，物体が排除した水（流体）の体積つまり直方体の体積\(V\)は\(V=Sl\)であらわされるので，\(F=F_2-F_1=\rho Vg\)となる。これが，浮力である。
コメント