【高校物理の要点】円運動

本記事では、『円運動』について解説していきたいと思います。

速さと角速度

速さと加速度：\(v=r\omega\)

速さ\(v\)[m/s]，半径\(r\)[m]，角速度\(\omega\)[rad/s]

物体が円周上を一定の速さで回る運動を等速円運動という。

円運動をする物体の単位時間当たりの回転角を角速度という。半径\(r\)[m]の円周上を角速度\(\omega\)[rad/s]で等速円運動しているとき，微小時間\(\it\Delta t\)の間に角度\(\it\Delta\theta\)だけ回転するとしたとすると，

$$\displaystyle\omega=\frac{\it\Delta \theta}{\it\Delta t}$$

が成り立つ。一方，この間に物体が通過する円弧の長さ\(\it\Delta l\)[m]は\(\it\Delta l=r\it\Delta\theta\)とあらわせるので，物体の速さ\(v\)[m/s]は，

$$\displaystyle v=\frac{\it\Delta l}{\it\Delta t}=r\frac{\it\Delta\theta}{\it\Delta t}$$

となる。これより，

$$v=r\omega$$

が成りたつ。

周期と回転数

周期と回転数

　\(\displaystyle T=\frac{2\pi r}{v}=\frac{2\pi}{\omega}\)

　\(\displaystyle n=\frac{1}{T}\)

周期\(T\)[s]，半径\(r\)[m]，速さ\(v\)[m/s]，角速度\(\omega\)[rad/s]，回転数\(n\)[Hz]

等速円運動する物体が1回転するのに必要な時間を周期という。等速円運動の半径を\(r\)[m]，角速度を\(\omega\)[rad/s]，速さを\(v\)[m/s]，周期を\(T\)[s]とすると，1回転したときの物体の移動距離は円周\(2\pi r\)[m]であるから

$$T=\frac{2\pi r}{v}$$

とあらわせる。また，\(v=r\omega\)より，以上の周期の公式は，

$$T=\frac{2\pi}{\omega}$$

と書き変えられる。

1秒当たりの回転の回数を回転数という。回転数\(n\)[Hz]と周期\(T\)の関係は，

$$n=\frac{1}{T}$$

となる。

等速円運動の加速度

等速円運動の加速度：\(\displaystyle a=r\omega^2=\frac{v^2}{r}\)

加速度\(a\)[m/s²]，半径\(r\)[m]，角速度\(\omega\)[rad/s]，速さ\(v\)[m/s]

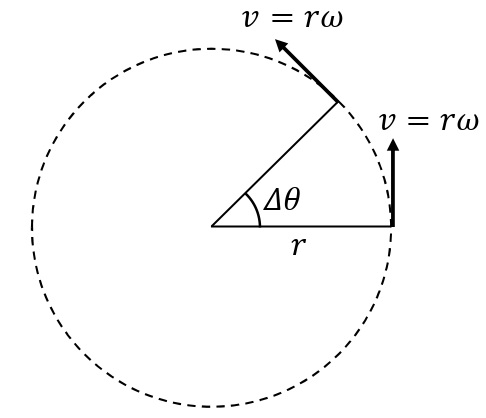
等速円運動では，速さは一定だが，その向きは常に変化しているので，速度自体は変化している。つまり，加速度が生じていることがわかる。半径\(r\)[m]，速さ\(v=r\omega\)の等速円運動について考える。\(\it\Delta t\)[s]の間に角\(\it\Delta\theta=\omega\it\Delta t\)[rad]だけ回転し，速度が\(\overrightarrow{v}\)[m/s]から\(\overrightarrow{v’}\)[m/s]になったとき，速度の向きも\(\it\Delta \theta\)だけ方向を変える。

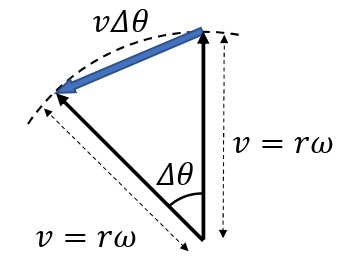
速度の変化\(\it\Delta \overrightarrow{v}=\overrightarrow{v’}-\overrightarrow{v}\)の大きさは，経過時間\(\it\Delta t\)を短くしていくと，下図より\(\it\Delta v≒v\it\Delta\theta\)に近似することができるので，加速度\(\overrightarrow{a}\)[m/s²]の大きさ\(a\)は，

\begin{eqnarray}a=\dfrac{\it\Delta v}{\it\Delta t}&≒&\dfrac{v\it\Delta \theta}{\it\Delta t}\\&=&v\times\dfrac{\it\Delta \theta}{\it\Delta t}\\&=&v\omega\\&=&r\omega^2=\dfrac{v^2}{r}\end{eqnarray}

とあらわすことができる。また，\(\it\Delta t\)を十分小さくしたとき，加速度の向きは速度の向きと直行するので，円の中心に向いていることがわかる。

等速円運動の運動方程式

等速円運動の運動方程式：
\(mr\omega^2=F\)　または　\(\displaystyle m\frac{v^2}{r}=F\)

質量\(m\)[kg]，半径\(r\)[m]，角速度\(\omega\)[rad/s]，速さ\(v\)[m/s]，向心力\(F\)[N]

物体が等速円運動しているとき，物体は常に中心方向に一定の大きさの加速度\(\overrightarrow{a}\)を持っている。この向心加速度を引き起こす，円の中心へ向かう向きにはたらく力\(\overrightarrow{F}\)を向心力という。

質量\(m\)[kg]の物体が半径\(r\)[m]，速さ\(v=r\omega\)[m/s]の等速円運動をしているとき，向心力の大きさを\(F\)[N]とすると，等速円運動の中心方向に対する運動方程式は

$$mr\omega^2=F　または　m\frac{v^2}{r}=F$$

となる。

鉛直面内の円運動

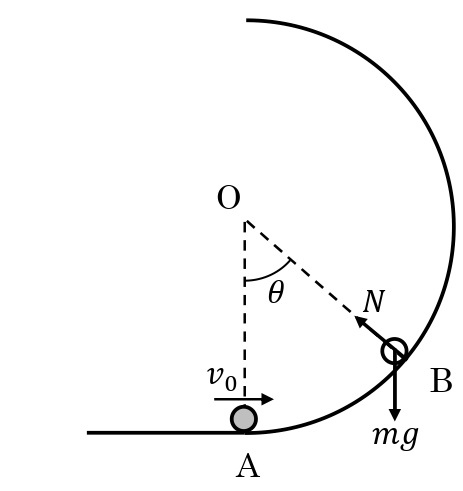
速さが一定とならない円運動でも，向心加速度\(a=\dfrac{v^2}{r}\)を使うことができる。例えば，半径\(r\)[m]のなめらかな半円筒の内面の最下点Aに向かって，質量\(m\)[kg]の小球を水平方向に速さ\(v_0\)[m/s]ですべらせる。最下点Aから角\(\theta\)だけ回転した点Bにおける速さを\(v_\theta\)とすると，エネルギー保存則より，

\begin{eqnarray}\dfrac{1}{2}mv_0^2&=&\dfrac{1}{2}mv_\theta^2+mgr(1-\cos\theta)\\v_\theta&=&\sqrt{v_0^2-2gr(1-\cos\theta)}\end{eqnarray}

とあらわせる。ここで，小物体にはたらく垂直抗力を\(N\)とすると，点Bにおける向心方向の運動方程式は，

$$m\frac{v_\theta^2}{r}=N-mg\cos\theta$$

と書きあらわすことができる。\(v_\theta=\sqrt{v_0^2-2gr(1-\cos\theta)}\)を代入すると，小球にはたらく垂直抗力\(N\)は，

\begin{eqnarray}m\dfrac{v_0^2-2gr(1-\cos\theta)}{r}&=&N-mg\cos\theta\\ N&=&m\dfrac{v_0^2}{r}-mg(2-3\cos\theta)\end{eqnarray}

となる。

小球が半円筒の内面から離れるときの角度\(\theta_0\)を求めてみよう。半円筒の内面から離れるとき\(N=0\)となることから，

\begin{eqnarray}0&=&m\dfrac{v_0^2}{r}-mg(2-3\cos\theta_0)\\ \cos\theta_0&=&\dfrac{2}{3}-\dfrac{v_0^2}{3gr}\end{eqnarray}
となる。

次に，小球が半円筒の最高点を通過する条件を求めてみよう。垂直抗力\(N\)が最小値をとるのは\(\theta=\pi\)のときである。このとき，\(N_{\rm min}=m\dfrac{v_0^2}{r}-5mg\)となる。最高点を通過する（最高点まで半円筒から離れない）条件は\(N_{\rm min}>0\)であるので，\begin{eqnarray}N_{\rm min}=m\dfrac{v_0^2}{r}-5mg&>&0\\ v_0&>&\sqrt{5gr}\end{eqnarray}
となる。よって，\(v_0>\sqrt{5gr}\)のとき，半円筒を離れることなく最高点を通過する。