【高校物理の要点】波と媒質の運動～波動の基本原理・横波と縦波・重ね合わせの原理・定在波・自由端反射と固定端反射～

本記事では、『波と媒質の運動～波動の基本原理・横波と縦波・重ね合わせの原理・定在波・自由端反射と固定端反射～』について解説していきたいと思います。

波動の基本原理

ある点で生じた振動が次々と周囲に伝わる現象を波または波動という。水面を伝わる波における水，空気を伝わる音における空気のように振動を伝える物質を媒質，媒質中で波が発生する点を波源という。波とは，媒質自体がある特定の向きに移動するのではなく，波源の振動がそのまわりに次々とと伝わっていく現象である。

正弦波と波の要素

波の要素

　\(v=f\lambda\)
　\(\displaystyle f=\frac{1}{T}\)

波の要素\(v\)[m/s]，振動数\(f\)[Hz]，波長\(\lambda\)[m]，周期\(T\)[s]

ある場所で単振動が起こり，その振動が周囲の媒質を伝わっていくとする。このとき単振動によって生じる波形は下図のような正弦曲線となる。このような波動を正弦波という。

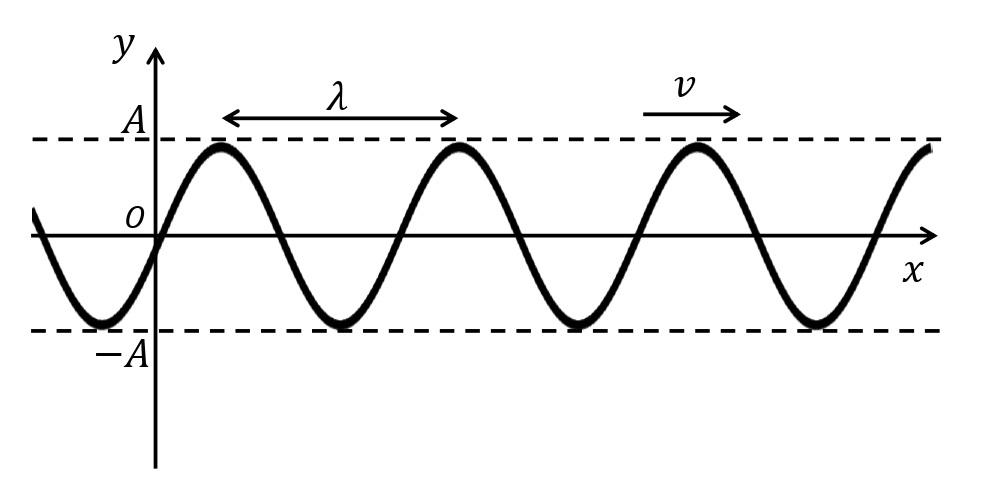
正弦波において波形の最も高い場所を山，最も低い場所を谷という。山の高さもしくは谷の深さを振幅（上図における\(A\)[m]）という。

媒質の振動1回にかかる時間\(T\)[s]を周期，単位時間あたりの振動の回数\(f\)[1/s]を振動数という。振動数の単位[1/s]にはヘルツ(Hz)を用いる。周期\(T\)[s]と振動数\(f\)[Hz]には，

\begin{eqnarray}f=\frac{1}{T}\end{eqnarray}

という関係がある。

隣り合う山と山の距離\(\lambda\)[m]を波長という。波が媒質中を伝わる速さを\(v\)[m/s]とすると，1周期\(T\)[s]の間に1波長\(\lambda\)[m]だけ進むので，\(vT=\lambda\)が成り立つ。ここで，\(f=\dfrac{1}{T}\)を用いると，

\begin{eqnarray}v=f\lambda\end{eqnarray}

となる。

波のグラフ

ある時刻の位置\(x\)[m]と媒質の変位\(y\)[m]の関係を表すグラフを\(y\)-\(x\)図という。一方，ある位置での，時間\(t\)[s]と媒質の変位\(y\)[m]の関係を表すグラフを\(y\)-\(t\)図という。

横波と縦波

媒質の振動方向が，波の進行方向に対して垂直である波を横波という。一方，媒質の振動方向が，波の進行方向に対して平行である波を縦波という。

縦波は，媒質が密集した部分(密部)とまばらな部分(疎部)のくり返しが伝わるので， 疎密波ともいわれる。縦波は，縦波のまま波形を図示するのが難しい。進行方向に\(x\)軸， それに垂直に\(y\)軸をとり，振動方向を\(y\)方向で表し，横波のように図示する。

＜縦波の横波表示の例＞

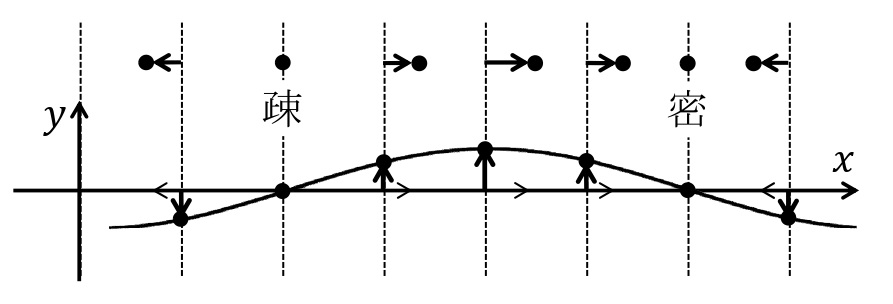
縦波における\(x\)軸上を正の向きに伝わる縦波の，ある時刻における疎密の状態を示したものである。図中の破線- – -は，媒質の各点のつりあいの位置を表している。

ある時刻における縦波の状態のつりあいの位置からの変位を，反時計まわりに\(90^\circ\)回転させて，\(y\)方向への変位として図に示すと下図のように縦波を横波表示することができる。

重ね合わせの原理

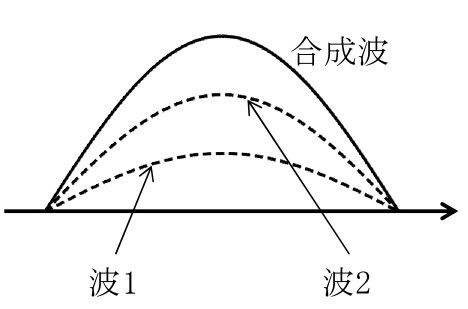
複数の波が重ね合わせによってできる波を合成波という。2つの波が出あった場所における変位\(y\)は，それぞれの波の変位\(y_1\)，\(y_2\)の和になっている。

\begin{eqnarray}y=y_1+y_2\end{eqnarray}

これを波の重ねあわせの原理という。

＜重ね合わせの原理の例＞

定在波

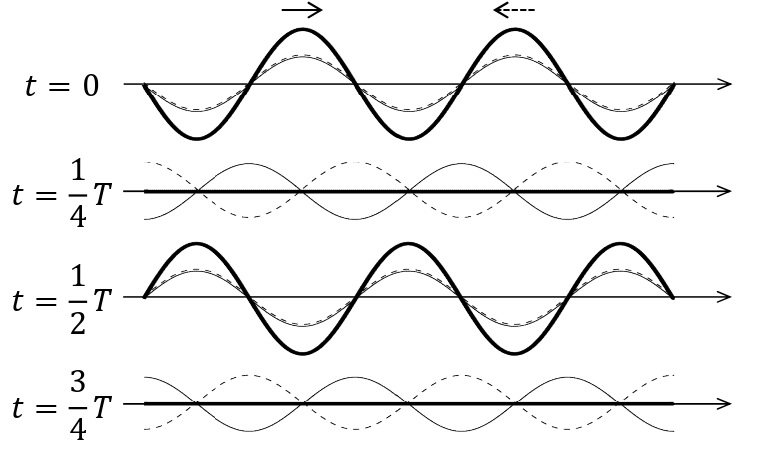
振幅・波長が等しい正弦波が，反対の向きに同じ速さで進むとき，合成波はどちらにも進まないように見える。このような波を定常波（定在波）という。

定在波において，まったく振動しない所を節，最大振幅で振動している点を腹という。定在波をつくる元の波の波長を\(\lambda\)[m]とすると，隣り合う腹と腹，節と節の間隔は\(\displaystyle\frac{\lambda}{2}\)[m]となる。

自由端反射・固定端反射

波は媒質の端や異なる媒質との境界で反射する。反射する前の波を入射波，反射により向きを変えて進む波を反射波と呼ぶ。

自由に動くことができる媒質の端を自由端という。自由端で反射した波は，反射面を超えた部分が，そのまま折り返される。これを自由端反射という。

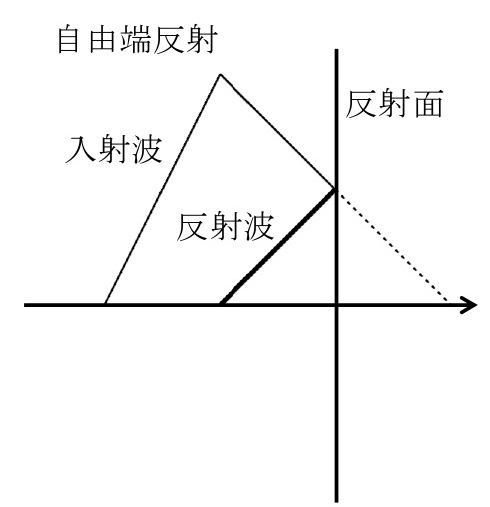
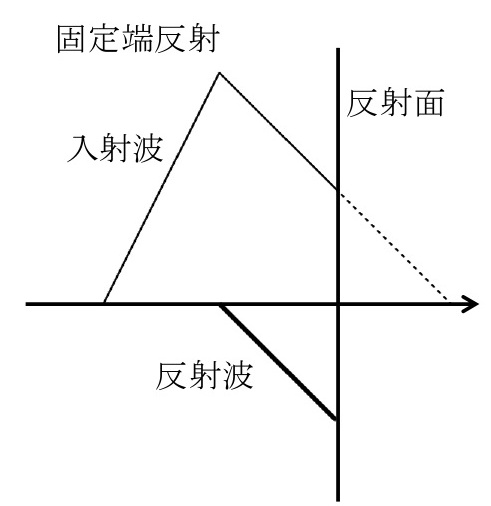
媒質が固定され振動できない端を固定端という。固定端で反射した波は，反射面を超えた部分が，変位の符号が反転して折り返される。これを固定端反射という。