【高校物理の要点】交流～コイルの回転と交流の発生・交流回路・変圧器・電気振動・電磁波～

本記事では、『交流～コイルの回転と交流の発生・交流回路・変圧器・電気振動・電磁波～』について解説していきたいと思います。

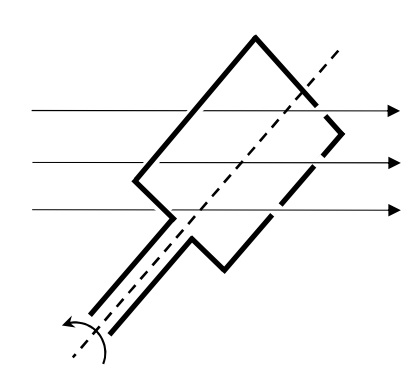
コイルの回転と交流の発生

図のように，磁束密度\(B\)[T]の一様な磁場中において，面積\(S\)[m²]の1巻きコイルを角速度\(\omega\)[rad/s]で回転させる。時刻0においてコイルの面が磁場と垂直になったとする。このとき，コイルは時間\(t\)[s]の間に\(\omega t\)[rad]だけ回転するので，時刻\(t\)[s]のときにコイルを貫く磁束は\(\it\Phi=BS\cos\omega t\)[Wb]と表すことができる。このコイルに発生する誘導起電力はファラデーの電磁誘導の法則から，

\begin{eqnarray}\displaystyle V&=&-\frac{\it\Delta\Phi}{\it\Delta t}\\ &=&-\frac{BS\cos\left\{\omega(t+\it\Delta t\rm)\right\}-\it BS\cos\omega t}{\it\Delta t}\\ &=&-\frac{BS\left(\cos\omega t\cdot\cos\omega\it\Delta t-\sin\omega t\cdot\sin\omega\it\Delta t\right)-BS\cos\omega t}{\it\Delta t}\end{eqnarray}

となる。ここで，\(\omega\it\Delta t\)は非常に小さいので，\(\cos\omega\it\Delta t≒\rm1\)，\(\sin\omega\it\Delta t≒\omega\it\Delta t\)と近似すると，

\begin{eqnarray}\displaystyle V&=&-\frac{BS(\cos\omega t-\sin\omega t\times\it\omega\Delta t\rm)-\it BS\cos\omega t}{\it\Delta t}\\ &=&BS\omega\sin\omega t\\ &=&V_0\sin\omega t\end{eqnarray}

と表すことができる。ただし，\(BS\omega=V_0\)である。このように，周期的に向きが変わる電圧を交流電圧という。\(V=V_0\sin\omega t\)において角速度\(\omega\)[rad/s]を交流電圧の角周波数といい，交流電圧が1回振動するのに要する時間\(\displaystyle T=\frac{2\pi}{\omega}\)[s]を交流電圧の周期，交流電圧が1秒間に振動する回数\(\displaystyle f=\frac{1}{T}=\frac{\omega}{2\pi}\)[Hz]を周波数という。

交流回路

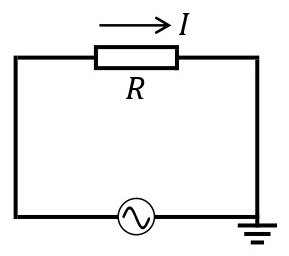
交流と抵抗

交流電圧が\(V=V_0\sin\omega t\)で表される交流電源に抵抗\(R\)[Ω]を接続する。流れる交流電流を\(I\)[A]とすると，オームの法則\(V=IR\)より，

\begin{eqnarray}\displaystyle I&=&\frac{V}{R}\\ &=&\frac{V_0}{R}\sin\omega t \end{eqnarray}

と表せる。以上より，電流の時間変化も電圧\(V\)と同様に正弦関数で表され，電圧の位相と電流の位相は一致していることがわかる。電流の最大値を\(I_0\)とすると，\(\displaystyle I_0=\frac{V_0}{R}\)となる。

抵抗で消費される電力は，\(\displaystyle P=IV=I_0V_0\sin^2\omega t=\frac{I_0V_0}{2}(1-\cos2\omega t)\)と表すことができる。ここで，交流電圧の実効値を\(\displaystyle V_{\rm e}=\frac{V_0}{\sqrt{2}}\)，交流電流の実効値を\(\displaystyle I_{\rm e}=\frac{I_0}{\sqrt{2}}\)とすると，消費電力の平均値\(\displaystyle \overline{P}=\frac{I_0V_0}{2}=V_{\rm e}I_{\rm e}\)となる。実効値を用いると，電力やオームの法則の計算を直流の場合と同様に行うことができる。

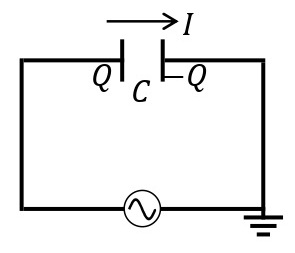
交流とコンデンサー

交流電圧が\(V=V_0\sin\omega t\)で表される交流電源に電気容量\(C\)[F]のコンデンサーを接続する。コンデンサーに蓄えられた電荷を\(Q\)[C]とすると，キルヒホッフの法則より，

\begin{eqnarray}\displaystyle V&=&\frac{Q}{C}\\ Q&=&CV_0\sin\omega t \end{eqnarray}

となる。ここで，回路に流れる電を\(I\)[A]とすると，

\begin{eqnarray}\displaystyle I&=&\frac{dQ}{dt}=\omega CV_0\cos\omega t\\ &=&\omega CV_0\sin\left(\omega t+\frac{\pi}{2}\right) \end{eqnarray}

と表せる。以上より，コンデンサーに流れ込む電流の位相は，コンデンサーに加わる電圧よりも\(\displaystyle \frac{\pi}{2}\)進んでいることがわかる。電流の最大値を\(I_0\)とすると，\(\displaystyle V_0=\frac{1}{\omega C}I_0\)となる。\(\displaystyle\frac{1}{\omega C}\)は抵抗と同じ次元を持つ物理量で，コンデンサーのリアクタンスという。コンデンサーの消費電力は\(\displaystyle P=IV=I_0V_0\sin\omega t\cos\omega t=\frac{I_0V_0}{2}\sin2\omega t\)と表せるので，その平均値は\(\overline{P}=0\)となる。

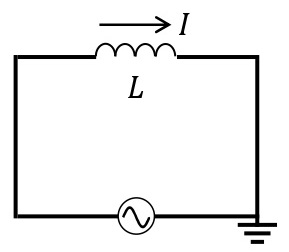
交流とコイル

交流電源に自己インダクタンスが\(L\)[H]のコイルを接続する。コイルに流れる電流を\(I=I_0\sin\omega t\)[A]とすると，交流電源の電圧を\(V\)[V]とすると，キルヒホッフの法則より，

\begin{eqnarray}\displaystyle V&=&L\frac{dI}{dt}=\omega LI_0\cos\omega t\\ &=&\omega LI_0\sin\left(\omega t+\frac{\pi}{2}\right) \end{eqnarray}

と表せる。以上より，コイルに流れる電流の位相は，コイルに加わる電圧よりも\(\displaystyle\frac{\pi}{2}\)遅れていることがわかる。電圧の最大値を\(V_0\)とすると，\(V_0=\omega LI_0\)となる。\(\omega L\)を，コイルのリアクタンスという。コイルの消費電力は\(\displaystyle P=IV=I_0V_0\sin\omega t\cos\omega t=\frac{I_0V_0}{2}\sin2\omega t\)と表せるので，その平均値は\(\overline{P}=0\)となる。

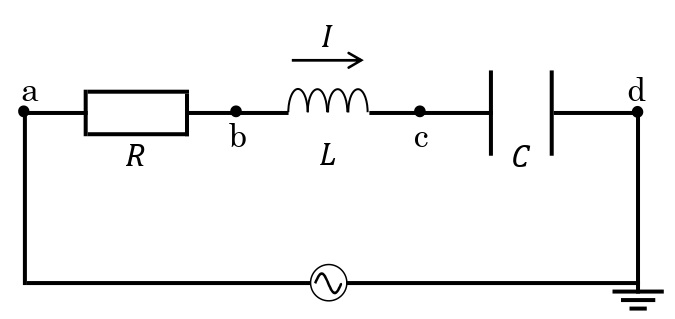
交流のRLC直列回路

下図のように抵抗値\(R\)[Ω]，自己インダクタンス\(L\)[H]のコイル，電気容量\(C\)[F]のコンデンサーが直列に交流に接続されている。回路に流れる電流を\(I=I_0\sin\omega t\)とする。

抵抗にかかる電圧を\(V_R\)(点bに対する点aの電位)とすると，オームの法則より，

\begin{eqnarray}\displaystyle V_R=RI_0\sin\omega t \end{eqnarray}

コイルにかかる電圧を\(V_L\)(点cに対する点bの電位)とすると，コイルのリアクタンスが\(\omega L\)であり，電流の位相より\(\displaystyle\frac{\pi}{2}\)進むので，

\begin{eqnarray}\displaystyle V_L&=&\omega LI_0\sin\left(\omega t+\frac{\pi}{2}\right)\\ &=&\omega LI_0\cos\omega t \end{eqnarray}

コンデンサーにかかる電圧を\(V_C\)(点dに対する点cの電位)とすると，コンデンサーのリアクタンスが\(\displaystyle\frac{1}{\omega C}\)であり，電流の位相より\(\displaystyle\frac{\pi}{2}\)遅れるので，

\begin{eqnarray}\displaystyle V_C&=&\frac{I_0}{\omega C}\sin\left(\omega t-\frac{\pi}{2}\right)\\ &=&-\frac{I_0}{\omega C}\cos\omega t \end{eqnarray}

電源電圧を\(V\)[V]とすると，\(V=V_R+V_L+V_C\)と表せるので，

\begin{eqnarray}\displaystyle V&=&V_R+V_L+V_C\\ &=&RI_0\sin\omega t+\omega LI_0\cos\omega t-\frac{I_0}{\omega C}\cos\omega t\\ &=&I_0\left\{R\sin\omega t+\left(\omega L-\frac{1}{\omega C}\right)\cos\omega t\right\} \end{eqnarray}

となる。ここで，三角関数の合成を用いて変形すると，

\begin{eqnarray}\displaystyle V&=I_0\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}\sin(\omega t+\delta) \end{eqnarray}

と表せる。ただし，\(\displaystyle\tan\delta=\frac{\omega L-\frac{1}{\omega C}}{R}\)である。

電源の電圧の最大値を\(V_0\)[V]とすると，\(\displaystyle Z=\frac{V_0}{I_0}=\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}\)をこの回路のインピーダンスという。

インピーダンスは，\(\displaystyle\omega L=\frac{1}{\omega C}\)のときに最小になり，流れる電流は最大となる。この現象を電気回路の共振という。このときの角周波数を\(\omega_0\)とすると，\(\displaystyle\omega_0=\frac{1}{\sqrt{CL}}\)となる。よって，共振するときの周波数（共振周波数）は\(\displaystyle f=\frac{1}{2\pi\sqrt{LC}}\)と表せる。

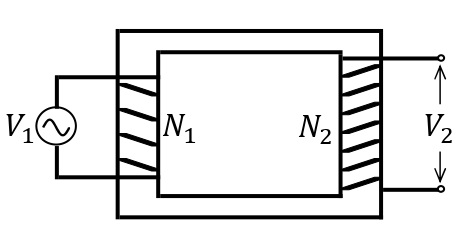
変圧器

2つのコイルの間の相互誘導を利用し，交流の電圧を変える装置を変圧器（トランス）という。変圧器は，巻数が異なるコイルを共通の鉄心に巻きつけた構造をしている。巻き数\(N_1\)の一次コイルに交流電流が流れると，巻き数\(N_2\)の二次コイルを貫く磁束が変化するため，二次コイルに誘導起電力が生じる。一次コイル，二次コイルの交流電圧の実効値を\(V_{\rm1e}\)[V]，\(V_{\rm2e}\)[V]とすると，\(\displaystyle\frac{V_{\rm1e}}{V_{\rm2e}}=\frac{N_1}{N_2}\)の関係が成り立つ。このように，変圧器はコイルの巻き数の比を変えることで，電圧を自由に変えることができる。

電力を損失なく伝えられる理想的な変圧器の場合，一次コイルの電圧と電流の実効値を\(V_{\rm1e}\)[V]，\(I_{\rm1e}\)[A]，二次コイルの電圧と電流の実効値をそれぞれ\(V_{\rm2e}\)[V]，\(I_{\rm2e}\)[A]とすると，\(V_{\rm1e}I_{\rm1e}=V_{\rm2e}I_{\rm2e}\)の関係が成り立つ。

電気振動

図のように，電荷\(Q_0\)[C]が蓄えられている電気容量\(C\)[F]のコンデンサーを自己インダクタンス\(L\)[H]のコイルと接続する。スイッチを入れてから時刻\(t\)[s]が経過した後のコンデンサーに蓄えられている電荷を\(Q\)[C]，回路に流れている電流を\(I\)[A]とすると，キルヒホッフの法則から，

\begin{eqnarray}\displaystyle -L\frac{dI}{dt}&=&\frac{Q}{C}\\ \frac{dI}{dt}&=&-\frac{Q}{LC}\end{eqnarray}

と表すことができる。ここで，回路に流れる電流\(I\)は電荷\(Q\)の減少速度に等しいので，\(\displaystyle I=-\frac{dQ}{dt}\)が成り立つ。よって，

\begin{eqnarray}\displaystyle \frac{d^2Q}{dt^2}=-\frac{1}{LC}Q \end{eqnarray}

となる。これは，単振動の式\(\displaystyle\frac{d^2x}{dt^2}=-\omega^2x\)と同じ形をしているので，\(\displaystyle\omega=\frac{1}{\sqrt{LC}}\)として，\(Q=Q_0\cos\omega t\)，\(I=Q_0\omega\sin\omega t\)と表すことができる。これより，コンデンサーに蓄えられた電荷や回路に流れる電流は周期\(\displaystyle T=\frac{2\pi}{\omega}=2\pi\sqrt{LC}\)を周期として変化していることがわかる。この現象を電気振動という。この振動回路の周波数\(\displaystyle f=\frac{1}{T}=\frac{1}{2\pi\sqrt{LC}}\)[Hz]を，固有周波数という。

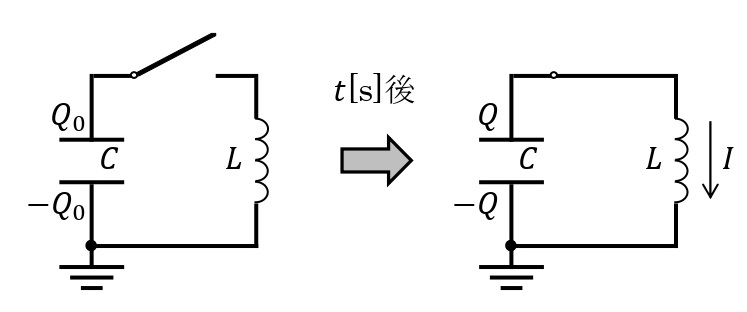
電気振動では，コンデンサーのエネルギー\(E_C\)[J]とコイルのエネルギー\(E_L\)[J]の和は一定に保たれる。以上の回路の場合，\(Q=Q_0\cos\omega t\)，\(I=Q_0\omega\sin\omega t\)，\(\displaystyle\omega=\frac{1}{\sqrt{LC}}\)であるので，

\begin{eqnarray}\displaystyle E&=&E_C+E_L\\ &=&\frac{Q^2}{2C}+\frac{1}{2}LI^2\\ &=&\frac{Q_0}{2C}\cos^2\omega t+\frac{1}{2}LQ_0^2\omega^2\sin^2\omega t\\ &=&\frac{Q_0}{2C}\cos^2\omega t+\frac{1}{2}LQ_0^2\left(\frac{1}{\sqrt{LC}}\right)\sin^2\omega t\\ &=&\frac{Q_0^2}{2C} \end{eqnarray}

となる。実際には，導線やコイルなどに電気抵抗があり，ジュール熱が発生する。よって，エネルギーはしだいに減少するので電流は減衰する。

電磁波

ファラデーの電磁誘導の法則が示すように磁場が変動すると電場の変動を引き起こす。同様に，電場が変動すると磁場の変動を引き起こす。マクスウェルは，この電場 ・磁場の変化が横波として真空中でも伝わっていくと予言した。これを電磁波という。さらに，電磁波の伝わる速さ\(\displaystyle c=\frac{1}{\sqrt{\varepsilon_0\mu_0}}\)を計算し，これが光の速さの測定値と良く一致したことから光も電磁波の一種であると考えた。その後，ヘルツはこの波の発生を火花放電の実験によって，電磁波が反射，屈折等の光と同じ性質をもつことを確認した。

電磁波は，振動数の小さい(波長の長い)ほうから順に，電波，赤外線，可視光線，紫外線，X線，\(\gamma\)線と大きく分類される。「光」は狭い意味では可視光線だが，電磁波の意味で用いられることも多い。

電波

波長が0.1mm程度以上の電磁波であり，ラジオやテレビ放送等に使われ，波長短い方から超短波，短波，中波，長波，超長波と呼ばれる。波長が1m以下の伝播を特にマイクロ波といい，携帯電話等に使われる。

赤外線

波長が約\(7.7\times10^{-7}\)m～\(10^{-4}\)mであり，物体に当たると吸収されて熱エネルギーになりやすいという性質をもつ。そのため，熱線とも呼ばれる。物体からの熱放射に多く含まれ，太陽光にも多く含まれる。

可視光

可視光線は，人の目で感じることができる電磁波で，波長は約\(3.8\times10^{-7}\)m～\(7.7\times10^{-7}\)mである。波長の長さによって色が異なり，長い方から並べると赤→橙→黄→緑→青→藍→紫のようになる。

紫外線

波長が\(10^{-8}\)m～\(3.8\times10^{-4}\)mであり，人の肌の日焼けの原因となるなど，物質に化学変化を起こさせやすい性質をもつ。そのため，化学線とも呼ばれる。非常に高温の物体から放射され，太陽光にも含まれる。

X線，\(\gamma\)線

X線や\(\gamma\)線は波長がきわめて短く約\(10^{-8}\)m以下の電磁波である。これらは，物質をよく透過し，レントゲン写真や，物体の内部や結晶構造の解析，がん細胞に照射する放射線治療等に用いられる。多量のX線や\(\gamma\)線は人体に影響をおよぼすため注意して取り扱わなければならない。