本記事では、『力のつりあいとニュートンの運動の3法則~力のつりあい・慣性の法則・運動の法則・作用反作用の法則~』について解説していきたいと思います。

予備校講師ともくん
専門科目:物理
経歴:東北大学物理学科
→東北大学大学院理学研究科物理学専攻
→公務員(教職ではない)
→塾業界に転職
→予備校&塾に出講中のプロ講師
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
力のつりあい
力のつりあい
力の\(x\)成分の総和が\(0\)
\(F_{1x}+F_{2x}+F_{3x}+\cdots+F_{nx}=0\)
力の\(y\)成分の総和が\(0\)
\(F_{1y}+F_{2y}+F_{3y}+\cdots+F_{ny}=0\)
物体がいくつかの力\(\overrightarrow{F_1}\),\(\overrightarrow{F_2}\),\(\overrightarrow{F_3}\),\(\cdots\),\(\overrightarrow{F_n}\)を受けた状態で静止しているとき,この物体が受ける力はつり合っている,という。このとき,\(\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}\cdots\overrightarrow{F_n}=\overrightarrow{0}\)である。
力のつりあいの例1
糸が\(15\)Nの力で物体A (重さ\(40\)N) を引く。物体Aが静止しているとき,床がAに及ぼす垂直抗力の大きさ\(N\)[N]を求めよ。
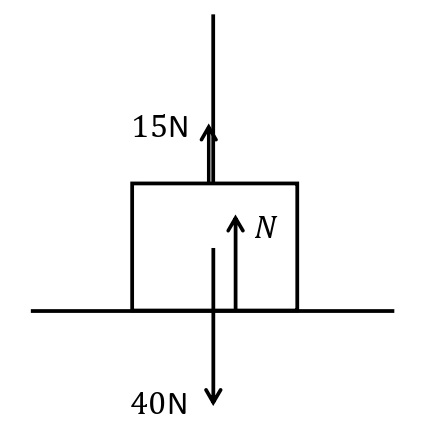
鉛直方向の力のつり合い
\begin{eqnarray}15+N-40&=&0\\ N&=&25\end{eqnarray}
よって,\(N=25\)N
力のつりあいの例2
軽い糸1と糸2に物体A(重さ\(20\)N)の小球をつけ下図のように静止させた。糸1が引く力\(T_1\)[N]と糸2が引く力\(T_2\)[N]を求めよ。
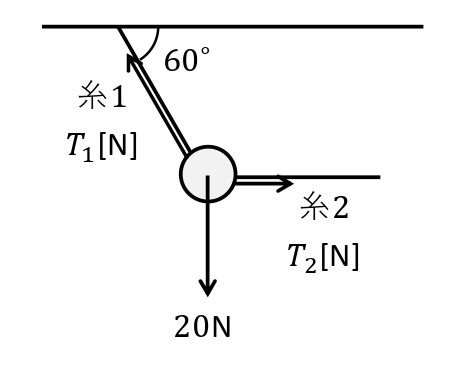
水平方向の力のつりあい:\(T_1\cos60^\circ-T_2=0\)
鉛直方向の力のつりあい:\(T_1\sin60^\circ-20=0\)
以上より,\(T_1=\dfrac{40}{\sqrt{3}}\)[N],\(T_2=\dfrac{20}{\sqrt{3}}\)[N]
ニュートンの運動の3法則
現在の物理学の基礎を気づいたのはニュートン(Isaac\ Newton)である。
- 運動の第一法則『慣性の法則』
- 運動の第二法則『運動の法則』
- 運動の第三法則『作用反作用の法則』
をニュートンの運動の3法則という。
運動の第一法則『慣性の法則』
慣性の法則
物体が受ける合力が\(\overrightarrow{0}\)のとき,物体は静止もしくは等速直線運動する。
物体は本来,静止の場合を含めて,その速度を保とうとする性質を持っている。これを慣性という。このような,物体にはたらく合力が\(\overrightarrow{0}\)もしくは,物体に力がはたらかない場合、物体の速度は変化しない(静止している物体は静止し続け、運動している物体は等速直線運動する)。これを慣性の法則という。
運動の第二法則『運動の法則』
運動の法則
質量\(m\)の物体が合力\(\overrightarrow{F}\)を受けることで,加速度\(\overrightarrow{a}\)で運動しているとき, $$m\overrightarrow{a}=\overrightarrow{F}$$
が成り立つ。
物体にいくつかの力がはたらくとき,物体にはそれらの合力\(\overrightarrow{F}\)の向きに加速度\(\overrightarrow{a}\)が生じる。その加速度の大きさは合力の大きさに比例し,物体の質量に\(m\)に反比例する。これを式で表すと,\(\overrightarrow{a}\propto\dfrac{\overrightarrow{F}}{m}\)となる。これを運動の法則という。
ここで,上の式の比例定数が1になる単位系(質量にkg,加速度にm/s²,力にN)を用いると,
$$m\overrightarrow{a}=\overrightarrow{F}$$
が成り立つ。これを運動方程式という。これは,運動の変化を引き起こす原因となる\(\overrightarrow{F}\)と,その結果発生する加速度\(\overrightarrow{a}\)との間の因果関係を表している。
運動方程式の例1
水平でなめらかな床の上に質量\(5\)kgの物体を置き,水平右向きに\(30\)Nの力を加えるとき,物体の加速度\(a\)[m/s²]を求めよ。
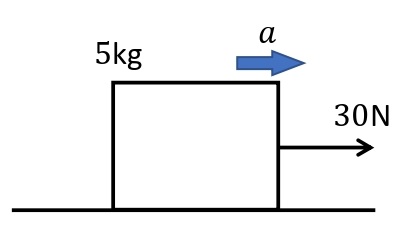
運動方程式
\begin{eqnarray}5a&=&30\\ a&=&6\end{eqnarray}
以上より,\(a=6\)m/s²
運動方程式の例2
水平でなめらかな床の上に質量\(5\)kgの物体Aと質量\(10\)kgの物体Bを置き,水平右向きに\(30\)Nの力を加えるとき,物体Aと物体Bの加速度\(a\)[m/s²]とAとBの間で及ぼしあう力の大きさ\(F\)[N]を求めよ。
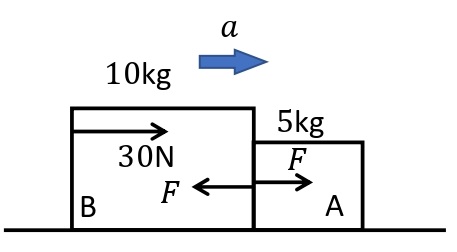
複数の物体が運動する問題においては,物体毎にはたらく力を考え,運動方程式をたてていくというのが原則である。
物体A:\(5a=F\)
物体B:\(10a=30-F\)
以上より,\(a=2\)m/s²,\(F=10\)N
運動の第三法則『作用反作用の法則』
作用反作用の法則
物体Aから物体Bに力をはたらかせると,物体Bから物体Aに,同じ作用線上で,大きさが等しく,向きが反対の力がはたらく。
物体Aが物体Bに力を及ぼしているとき,物体Bも物体Aに力を及ぼしている。このときの二つの力は,大きさは等しく互いに逆向きとなる。これを作用反作用の法則という。










コメント