【高校物理の要点】波の式～正弦波の式・正弦波の位相～

2024年6月8日2024年7月27日

このサイトはアフィリエイト広告（Amazonアソシエイト含む）を掲載しています。

本記事では、『波の式～正弦波の式・正弦波の位相～』について解説していきたいと思います。

筆者について

大学受験物理講師・ともくん

青森県出身。37歳。

経歴　東北大学物理学科→東北大学大学院理学研究科物理学専攻→公務員(教職ではない)→塾業界に転職。講師歴約10年(物理・数学)

歴代合格実績：旧帝大医学部、国公立大・私大医学部、東工大、旧帝大等多数

長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。

波の式

正の向きに進む正弦波

正弦波の式

　\(\displaystyle y=A\sin2\pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)\)

変位\(y\)[m]，振幅\(A\)[m]，時間\(t\)[s]，周期\(T\)[s]，位置\(x\)[m]，波長\(\lambda\)[m]

ある場所で単振動が起こり，その振動が正弦曲線を波形をもつ波が伝わっていくとする。この波を正弦波という。

単振動をする波源から，振幅を\(A\)[m]，周期を\(T\)[s]，波長を\(\lambda\)[m]の正弦波が\(x\)軸の正の向きに速さ\(v\)[m/s]で伝わっているとする。\(x=0\)にある波源の時刻\(t\)[s]での変位\(y\)[m]が単振動の式

\begin{eqnarray}\displaystyle y=A\sin\frac{2\pi}{T}t\cdots\cdots①\end{eqnarray}

で表されるとする。

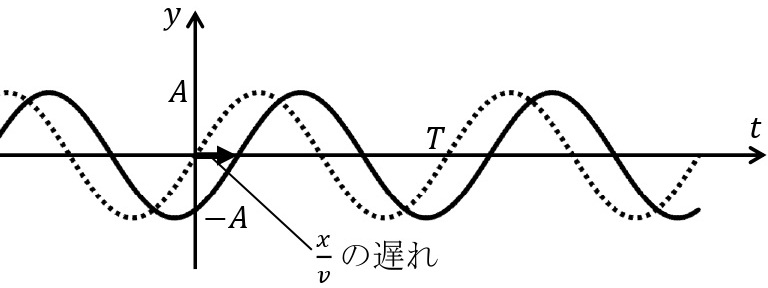
ここで，座標\(x\)[m]の位置における振動は，原点における振動よりも時間\(\displaystyle\frac{x}{v}\)[s]だけ遅れて伝わるので，時刻が\(t\)[s]での位置\(x\)[m]の変位\(y\)[m]は，時刻が\(\displaystyle t-\frac{x}{v}\)[s]での原点の変位と等しい。よって，①式の\(t\)を\(\displaystyle t-\frac{x}{v}\)で置き換えると，

\begin{eqnarray}\displaystyle y&=&A\sin\frac{2\pi}{T}\left(t-\frac{x}{v}\right)\\&=&A\sin2\pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)\end{eqnarray}
の式が得られる。

負の向きに進む正弦波

負の向きに速さ\(v\)[m/s]で伝わる正弦波では，座標\(x\)[m]の位置における振動は，原点における振動よりも時間\(\displaystyle \frac{x}{v}\)[s]だけ早く到達する。よって，原点での変位が\(\displaystyle y=A\sin\frac{2\pi}{T}t\)で与えられるとき，位置\(x\)[m]での変位は，

\begin{eqnarray}\displaystyle y&=&A\sin\frac{2\pi}{T}\left(t+\frac{x}{v}\right)\\&=&A\sin2\pi\left(\frac{t}{T}+\frac{x}{\lambda}\right)\end{eqnarray}
と表される。

正弦波の位相

\(\displaystyle y=A\sin2\pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)\)の式中の\(\sin\)の角度部分\(\displaystyle 2\pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)\)を波の位相と呼ぶ。

正弦波\(\displaystyle y=A\sin2\pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)\)において，\(x=x_0\)の点から波長\(m\lambda\)（\(m\)は整数）離れた位置にある\(x=x_0\pm\lambda，x_0\pm2\lambda，\cdots\)では，同じ振動を行う。これらの各点は互いに同位相であるという。

一方，\(x=x_0\)の点から波長\(\displaystyle \left(m+\frac{1}{2}\right)\lambda\)（\(m\)は整数）離れた位置にある\(\displaystyle x=x_0\pm\frac{1}{2}\lambda，x_0\pm\frac{3}{2}\lambda，\cdots\)では，常に変位が逆となる振動を行う。これらの各点は互いに逆位相であるという。