【高校物理の要点】電子と光（2）～X線の発生・ブラッグの反射条件・コンプトン効果・物質波

2025年1月2日2025年1月3日

このサイトはアフィリエイト広告（Amazonアソシエイト含む）を掲載しています。

本記事では、『電子と光（2）～X線の発生・ブラッグの反射条件・コンプトン効果・物質波』について解説していきたいと思います。

筆者について

大学受験物理講師・ともくん

青森県出身。38歳。

経歴　東北大学物理学科→東北大学大学院理学研究科物理学専攻→公務員(教職ではない)→塾業界に転職→3つの予備校＆塾をかけもつプロ講師(物理・数学)

歴代合格実績：旧帝大医学部、国公立大・私大医学部、東工大、旧帝大等多数

長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。

大学受験講師がおすすめする

物理の問題集＆オンライン教育サービス

大学受験物理講師がおすすめ！物理の問題集・参考書９選

家の近くの塾を探すなら学習塾情報サイト『塾選（ジュクセン）』がおすすめ

【高校生・大学受験】大学受験講師がおすすめする『オンライン個別』３選

【高校生・大学受験】大学受験講師がおすすめする『通信教育』４選

X線

19世紀末，レントゲンは放電管から正体不明の放射線が出ていることを発見し，それをX線と呼んだ。X線には次のような性質があることがわかっている。

蛍光物質を光らせる。
直進性があり，電場や磁場の影響を受けない。
電離作用がある。
強い透過力をもつ。

X線の発生

X線は，電子を高電圧で加速して金属に衝突させると発生させることができる。X線管から放射されるX線の強さと波長の関係を調べると，下図のようなX線スペクトルを得ることができる。

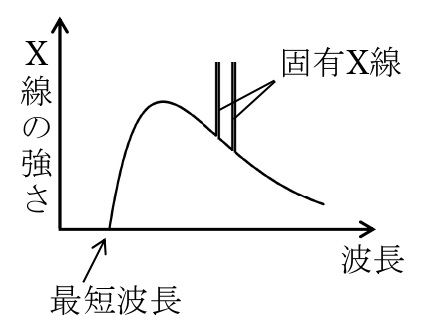
発生するX線は最短波長\(\lambda_{\rm{min}}\)[m]に始まり，これよりも長い波長のものを連続的に生じる。これを連続X線という。X線の最短波長は，電子のエネルギーがすべて1個のX線光子のエネルギーに変わるときに発生する。電子の初速度を0とし，加速電圧を\(V\)[V]とすると，

\begin{eqnarray} \displaystyle eV&=\frac{hc}{\lambda_{\rm{min}}}\\ \lambda_{\rm{min}}&=\frac{hc}{eV} \end{eqnarray}

が成り立ち，これより，最短波長は加速電圧\(V\)[V]によって決まることがわかる。

一方，特定の波長で鋭いピークが現れる。このピークの波長はターゲットの金属の材質によって決まり，このX線は特性X線(固有X線)と呼ばれる。

X線の波動性とブラッグの条件

X線回折

ラウエは，X線を薄い単結晶に当てたとき，写真フィルムに斑点上の干渉模様ができることを発見した。この斑点をラウエ斑点という。この実験により，X線は波動性をもつことがわかった。

ブラッグの実験

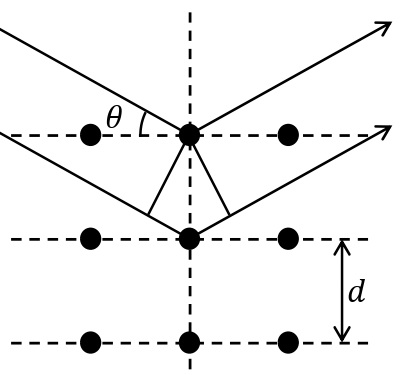
ブラッグの反射条件：\(2d\sin\theta=n\lambda\)　　\((n=1，2，\cdots)\)

格子面の間隔\(d\)[m]，格子面と入射X線とのなす角\(\theta\)，X線の波長\(\lambda\)[m]，正の整数\(n\)

ブラッグは，結晶中の原子によって散乱されたX線が干渉して強めあう条件を導き出した。格子面の間隔が\(d\)[m]の結晶に，波長\(\lambda\)[m]のX線を照射角\(\theta\)で入射させる。ある格子面で反射したX線とその下の面で反射するX線の経路差は\(2d\sin\theta\)[m]で表されるので，X線が強めあう条件は，

\begin{eqnarray}\displaystyle 2d\sin\theta&=m\lambda \end{eqnarray}

と表される。

X線の粒子性とコンプトン効果

光子の運動量：\(\displaystyle p=\frac{h\nu}{c}=\frac{h}{\lambda}\)

光子の運動量\(p\)[kg・m/s]，プランク定数\(h\)[J・s]，光の振動数\(\nu\)[Hz]，真空中の光速\(c\)[m/s]，光の波長\(\lambda\)[m]

物質にX線を当てると，X線は様々な方向に散乱される。散乱されたX線の波長はもとのX線の波長よりも長いものが含まれている。この現象をコンプトン効果という。

アインシュタインは，光子はエネルギー\(h\nu\)[J]をもつと同時に運動量\(\displaystyle p=\frac{h\nu}{\lambda}=\frac{h}{\lambda}\)[kg・m/s]をもつと考えた。

コンプトン効果は，X線を波動と考えると説明できない。しかし，このアインシュタインの運動量をもつ光子の考えにもとづくと，コンプトン効果を説明できる。

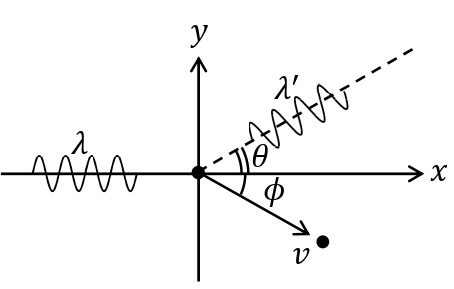
下図のように，質量\(m\)[kg]静止した電子に波長\(\lambda\)[m]のX線を当てる。電子が\(\phi\)の方向に速さ\(v\)で電子がはね飛ばされ，X線は入射方向に対して\(\theta\)の方向に散乱され，波長が\(\lambda’\)になったとする。X線には粒子性があり，エネルギー保存の法則とともに，運動量保存則が成り立つ。

エネルギー保存則：\(\displaystyle\frac{hc}{\lambda}=\frac{hc}{\lambda’}+\frac{1}{2}mv^2\)

\(x\)軸方向の運動量保存則：\(\displaystyle \frac{h}{\lambda}=\frac{h}{\lambda’}\cos\theta+mv\cos\phi\)

\(y\)軸方向の運動量保存則：\(\displaystyle 0=\frac{h}{\lambda’}\sin\theta-mv\sin\phi\)

となる。これらの式から\(v\)と\(\phi\)を消去すると，\(\lambda≒\lambda’\)のとき，

\begin{eqnarray}\displaystyle \it\Delta\lambda=\lambda’-\lambda=\frac{h}{mc}\rm(1-\it\cos\theta \rm ) \end{eqnarray}

と表すことができる。この計算結果が実験結果とよくあうことが示された。

粒子の波動性

物質波

ド・ブロイ波長：\(\displaystyle \lambda=\frac{h}{p}=\frac{h}{mv}\)

ド・ブロイ波長\(\lambda\)[m]，粒子の質量\(m\)[kg]，プランク定数\(h\)[J・s]，粒子の速さ\(v\)[m/s]，粒子の運動量\(p\)[kg・m/s]

ド・ブロイは，光やX線のような電磁波が粒子性をもつならば，逆に，電子のような粒子は波動性をもつと考えた。この波の波長\(\lambda\)[m]は，物質粒子の運動量を\(p\)[kg・m/s]，質量\(m\)[kg]，速さを\(v\)[m/s]とすると，\(\displaystyle\lambda=\frac{h}{p}=\frac{h}{mv}\)と表される。この波を物質波(ド・ブロイ波)という。

光や粒子はともに粒子性と，波動性をあわせもつ。このように一見すると相反する2つの性質をもつ現象を粒子と波動の二重性といわれる。