【高校物理の要点】万有引力～ケプラーの法則・万有引力・万有引力による位置エネルギー・宇宙速度～

本記事では、『万有引力～ケプラーの法則・万有引力・万有引力による位置エネルギー・宇宙速度～』について解説していきたいと思います。

ケプラーの法則

ケプラーは太陽系の惑星の運動に関する以下の3つの法則を見いだした。これらをケプラーの法則という。

ケプラーの法則

第一法則
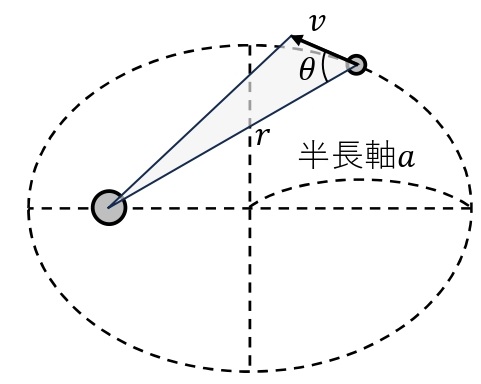
　惑星は太陽を1つの焦点とするだ円上を運動する。

第二法則
　惑星と太陽とを結ぶ線分が一定時間に通過する面積は一定である。 (面積速度一定の法則)。
$$\frac{1}{2}rv\sin\theta=一定$$

第三法則
　惑星の公転周期\(T\)の2乗と軌道だ円の長半径(半長軸の長さ)\(a\)の3乗の比は，すべての惑星で一定になる。
$$\frac{T^2}{a^3}=一定$$

万有引力

万有引力の法則：\(\displaystyle F=G\frac{Mm}{r^2}\)

万有引力\(F\)[N]，万有引力定数\(G\)[N・m²/kg²]，距離\(r\)[m]，物体の質量\(M\)，\(m\)[kg]

距離\(r\)[m]だけ離れた質量\(m\)[kg]，\(M\)[kg]の2物体間には，互いに引き合う向きに万有引力がはたらいている。万有引力定数を\(G\)[N・m²/kg²]とするとその大きさは

$$F=G\frac{Mm}{r^2}$$

とあらわされる。

地表近くの物体にはたらく重力は，地球との間の万有引力と地球の自転による遠心力の合力であらわされる。しかし，実際には，物体にはたらく遠心力は，大きさが最大となる赤道上でも\(\displaystyle \frac{1}{290}\)程度しかないため，重力は万有引力と等しいと考えてよい。地球の質量を\(M_E\)[kg]，半径を\(R_E\)[m]とすると，地球表面にある質量\(m\)[kg]の物体が受ける重力の大きさは，万有引力の法則より，次のように表すことができる。

$$mg=G\frac{M_Em}{R_E^2}$$

したがって，\(\displaystyle g=\frac{GM_E}{R_E^2}\)　または　\(GM_E=gR_E^2\)の式が得られる。

万有引力による位置エネルギー

万有引力による位置エネルギー：\(\displaystyle U=-G\frac{Mm}{r}\)

万有引力による位置エネルギー\(U\)[J]，万有引力定数\(G\)[N・m²/kg²]，距離\(r\)[m]，地球の質量\(M\)[kg]，物体の質量\(m\)[kg]

重力と同様に，万有引力も保存力である。つまり，万有引力がする仕事も経路に関係なく， 2点の位置だけで決まる。質量\(M\)[kg]の地球の中心Oから距離\(r\)[m]の位置にある，質量\(m\)[kg]の物体がもつ万有引力による位置エネルギーは，2物体が無限に離れているとき(無限遠)を基準として

$$U=-G\frac{Mm}{r}$$

とあらわせる。

力学的エネルギー保存則

物体が万有引力のみを受けて運動するとき，物体の力学的エネルギーは保存する。質量\(m\)[kg]の物体が，質量\(M\)[kg]の物体から万有引力を受けて速さ\(v\)[m/s]で運動しているとき，

$$\frac{1}{2}mv^2-G\frac{Mm}{r}=一定$$

が成り立つ。

宇宙速度

第一宇宙速度

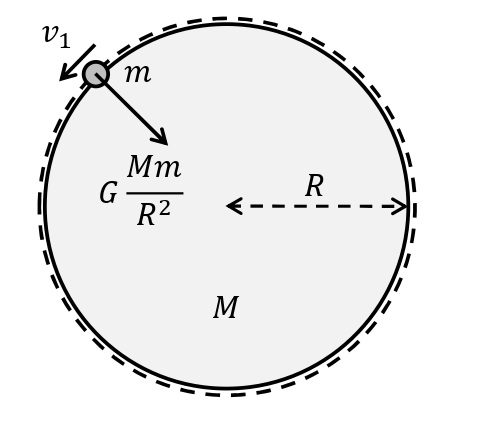
地球の表面すれすれの円軌道を回っている物体の速さを第一宇宙速度という。地球の質量を\(M\)[kg]，円軌道を回っている物体の質量を\(m\)[kg]，地球の半径を\(R\)[m]，第一宇宙速度を\(v_1\)[m/s]とすると，円運動の運動方程式より，
\begin{eqnarray}m\dfrac{v_1^2}{R}&=&G\dfrac{Mm}{R^2}\\ v_1&=&\sqrt{\dfrac{GM}{R}}\end{eqnarray}
と求まる。

第二宇宙速度

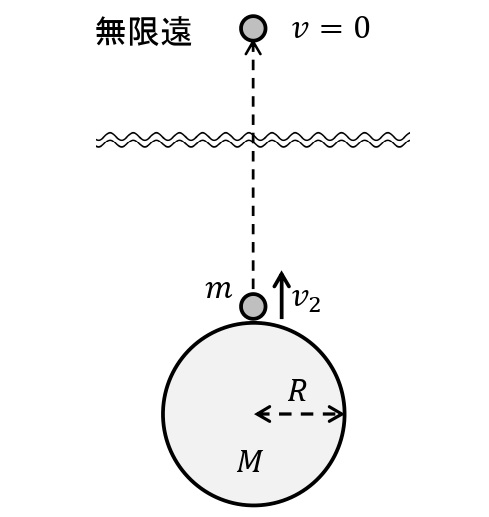
地上から打ち上げた人工衛星が，無限の遠方へ飛んでいくための最小の初速度を第二宇宙速度という。地球の質量を\(M\)[kg]，物体の質量を\(m\)[kg]，地球の半径を\(R\)[m]，第二宇宙速度を\(v_2\)[m/s]とする。第二宇宙速度をとるとき，無限遠の地点で速さが0となればよいので，エネルギー保存則より，
\begin{eqnarray}\dfrac{1}{2}mv_2^2-G\dfrac{Mm}{R}&=0&\\ v_2&=&\sqrt{\dfrac{2GM}{R}}\end{eqnarray}
と求まる。