本記事では、『落体の運動～自由落下・鉛直投げ下ろし・鉛直投げ上げ・水平投射・斜方投射～』について解説していきたいと思います。
大学受験物理講師・ともくん
青森県出身。37歳。
経歴 東北大学物理学科→東北大学大学院理学研究科物理学専攻→公務員(教職ではない)→塾業界に転職。講師歴約10年(物理・数学)
歴代合格実績：旧帝大医学部、国公立大・私大医学部、東工大、旧帝大等多数
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
重力加速度
地表付近で自由に運動している物体は，重力による鉛直下向きの加速度（大きさ\(g\)[m/s²]）を持っている。この加速度のことを重力加速度という。
自由落下
自由落下
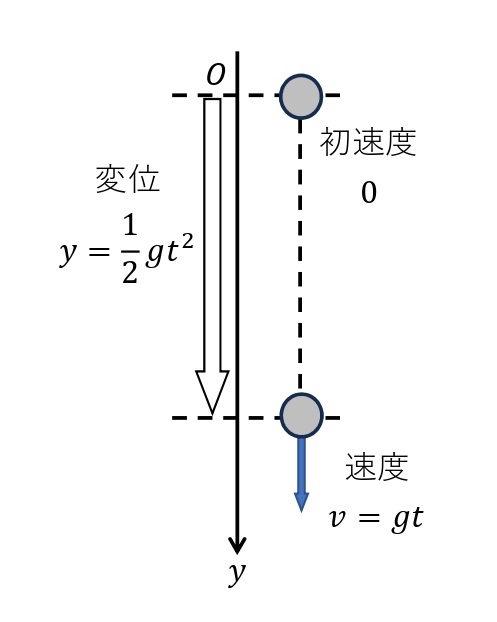
① \(v=gt\)
② \(\displaystyle y=\frac{1}{2}gt^2\)
③ \(v^2=2gy\)
物体が重力だけを受け，初速度0で鉛直に落下する運動を自由落下という。自由落下は，初速度の大きさ0，加速度が鉛直下向きに大きさ\(g\)[m/s²]の等加速度直線運動である。自由落下を始める点を原点として，鉛直下向きに\(y\)軸をとり，\(t\)[s]後の座標を\(y\)[m]，速度を\(v\)[m/s]とすると，上記の式が成りたつ。
鉛直投げ下ろし
鉛直投げ下ろし
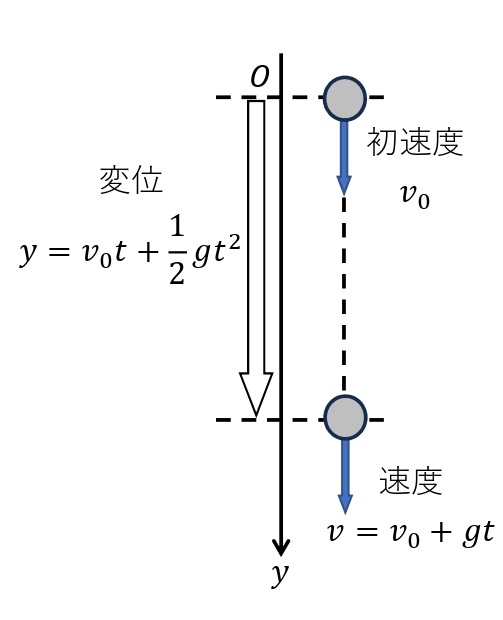
① \(v=v_0+gt\)
② \(\displaystyle y=v_0t+\frac{1}{2}gt^2\)
③ \(v^2-v_0^2=2gy\)
ある高さの点から鉛直下方に向けて，小球を初速度\(v_0\)[m/s]で投げ下ろす場合も，加速度が鉛直下向きに大きさ\(g\)[m/s²]の等加速度直線運動となる。投げおろした点を原点として，鉛直下向きに\(y\)軸をとり，\(t\)[s]後の座標を\(y\)[m]，速度を\(v\)[m/s]とすると，上記の式が成りたつ。
鉛直投げ上げ
鉛直投げ上げ
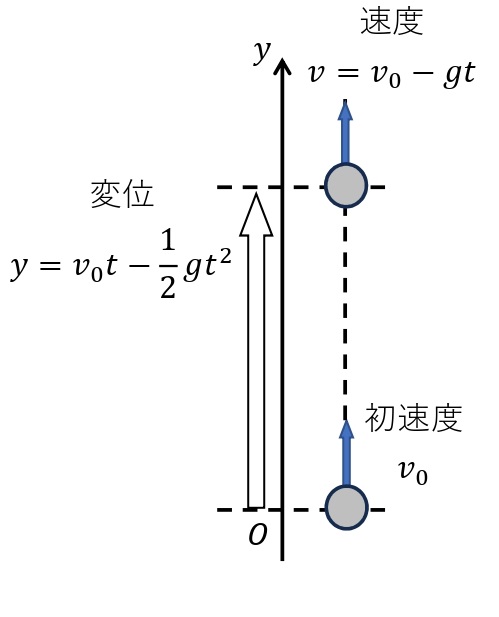
① \(v=v_0-gt\)
② \(\displaystyle y=v_0t-\frac{1}{2}gt^2\)
③ \(v^2-v_0^2=-2gy\)
ある高さの点から鉛直上方に向けて，小球を初速度\(v_0\)[m/s]で投げ上げる場合も，加速度が鉛直下向きに大きさ\(g\)[m/s²]の等加速度直線運動となる。投げ上げた点を原点として，鉛直上向きに\(y\)軸をとり，\(t\)[s]後の座標を\(y\)[m]，速度を\(v\)[m/s]とすると，上記の式が成りたつ。
水平投射
水平投射
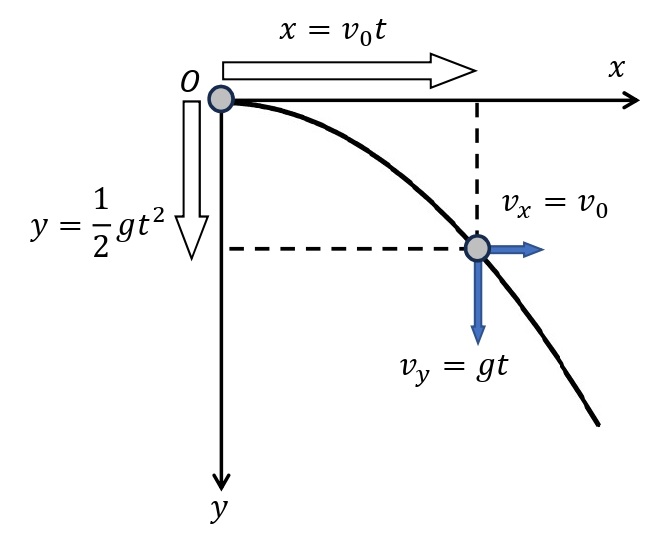
\(x\)軸方向：\(\left\{ \begin{array}{l} v_x=v_0 \\
x=v_0t \end{array} \right.\)
\(y\)軸方向：\(\displaystyle\left\{ \begin{array}{l} v_y=gt \\
y=\frac{1}{2}gt^2 \end{array} \right.\)
空中で物体に水平方向に大きさ\(v_0\)[m/s]の初速度を与えたときの運動を水平投射という。水平投射された物体の運動は，
- 水平方向は等速直線運動と同様の運動をしており，その速さは投げ出したときの速さ（初速度の大きさ）に等しい。
- 鉛直方向は自由落下と同様の運動をする。
の特徴を持つ。
投げ出した点を原点，水平方向に\(x\)軸，鉛直下向きに\(y\)軸をとる。\(t\)[s]後の小球の座標を\((\)\(x\)[m]，\(y\)[m]\()\)，\(x\)軸方向の速度を\(v_x\)[m/s]，\(y\)軸方向の速度を\(v_y\)[m/s]とすると，上記の式が成り立つ。
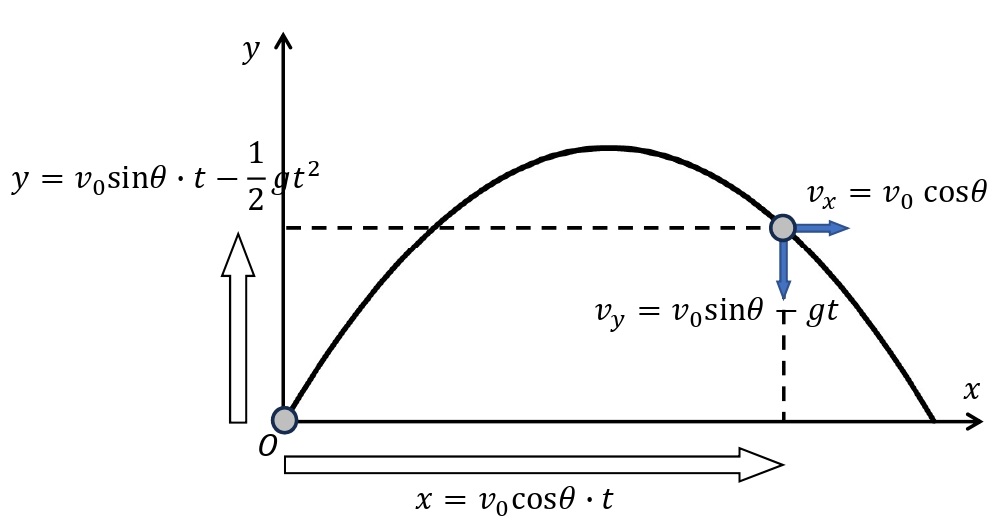
斜方投射
斜方投射
\(x\)軸方向：\(\left\{ \begin{array}{l} v_x=v_0\cos\theta \\ x=v_0\cos\theta\cdot t \end{array} \right.\)
\(y\)軸方向：\(\displaystyle\left\{ \begin{array}{l} v_y=v_0\sin\theta-gt \\ y=v_0\sin\theta\cdot t-\frac{1}{2}gt^2 \end{array} \right.\)
物体を斜めに投げ上げると，物体は放物線を描いて飛んでいき，やがて地面に達する。この運動を斜方投射という。斜方投射された物体の運動は，
- 水平方向には等速直線運動と同様の運動をしている。
- 鉛直方向には鉛直投げ上げと同様の運動をしている。
- 物体の運動の軌道は，最高点を頂点とし鉛直線を軸とする，上に凸の放物線となる。
の特徴を持つ。
小球を水平方向と角\(\theta\)をなす向きに，大きさ\(v_0\)[m/s]の初速度で投げたとする。投げ出した点を原点，水平方向に\(x\)軸，鉛直上向きに\(y\)軸をとる。\(t\)[s]後の小球の座標を\((\)\(x\)[m]，\(y\)[m]\()\)，\(x\)軸方向の速度を\(v_x\)[m/s]，\(y\)軸方向の速度を\(v_y\)[m/s]とすると，上記の式が成り立つ。
コメント