【高校物理の要点】仕事と力学的エネルギー

本記事では、『仕事と力学的エネルギー』について解説していきたいと思います。

仕事

仕事：\(W=Fx\cos\theta\)

仕事\(W\)[J]，力の大きさ\(F\)[N]，移動距離\(x\)[m]，力の向きと移動の向きがなす角\(\theta\)[\(^\circ\)]}

物体に大きさ\(F\)[N]の力を加えて，物体が力と同じ向きに距離\(x\)[m]移動させたとき，\(W=Fx\)をこの力が物体にした仕事という。

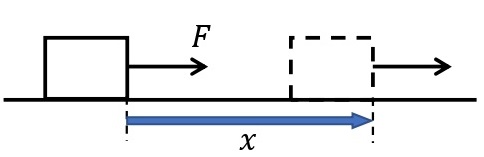
斜め上方に一定の力\(F\)を加え続けて物体を動かす場合，力の向きと物体の動く向きが異なる。その場合は，それらのなす角を\(\theta\)として，力\(F\)の物体の移動方向の分力\(F\cos\theta\)と移動距離\(x\)との積\(F\cos\theta\times x\)が，この力のした仕事となる。

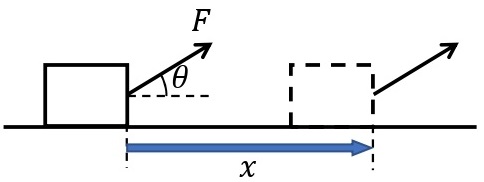
物体に力を加えていても，必ずしも物体に仕事をするわけではない。例えば，\(\theta=90^\circ\)のとき，\(\cos90^\circ=0\)となり，仕事\(W\)は0となる。また，移動距離\(x\)が0の場合も，仕事\(W\)は0となる。

仕事率

仕事率：\(\displaystyle P=\frac{W}{t}=Fv\)

仕事率\(P\)[W]，仕事\(W\)[J]，時間\(t\)[s]，力の大きさ\(F\)[N]，物体の速さ\(v\)[m/s]

単位時間当たりの仕事を仕事率という。時間\(t\)[s]で\(W\)[J]の仕事をするときの仕事率\(P\)[W]は，\(\displaystyle P=\frac{W}{t}\)の式で表される。

物体が一直線上で大きさ\(F\)[N]の力を受けて微小時間\(\it\Delta t\)[s]の間に\(\it\Delta x\)[m]進むとする。この間に力がする仕事\(W\)[J]は\(W=F\it\Delta x\)とあらわせるので，仕事率\(P\)[W]は\(\displaystyle P=\frac{F\it\Delta x}{\it\Delta t}\)とあらわすことができる。一方，速さ\(v\)[m/s]は\(\displaystyle \it\frac{\it\Delta x}{\it\Delta t}\)であるので，仕事率\(P\)[W]は\(\displaystyle P=\frac{F\it\Delta x}{\it\Delta t}=Fv\)と変形できる。

運動エネルギー

運動エネルギー：\(\displaystyle K=\frac{1}{2}mv^2\)

運動エネルギー\(K\)[J]，質量\(m\)[kg]，速さ\(v\)[m/s]

物体が\(E\)[J]の仕事をする能力をもつとき，物体は\(E\)[J]のエネルギーをもつという。一般に，運動している物体は，仕事をすることができる。つまり，エネルギーをもっている。このエネルギーを運動エネルギーという。

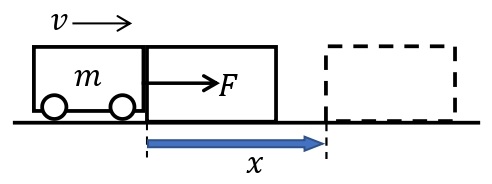
今，質量\(m\)[kg]の台車の前に物体を接触させて置き，初速\(v\)を与えて物体を押す場合を考える。ここでは，台車の進行方向を正とし，台車が物体を押す力の大きさ\(F\)[N]，静止するまでに移動する距離を\(x\)[m]とする。台車が物体を押す間，作用反作用の法則から，台車は物体から負の向きに大きさ\(F\)[N]の力を受けている。よって，台車の加速度を\(a\)[m/s²]とすると，台車の運動方程式は\(ma=-F\)とあらわすことができる。よって，

\begin{eqnarray}a=-\dfrac{F}{m}\end{eqnarray}

となる。ここで，等加速度直線運動の公式に代入すると，

\begin{eqnarray}0^2-v^2&=&2\times \left(-\dfrac{F}{m}\right)\times x\\ Fx&=&\dfrac{1}{2}mv^2\end{eqnarray}

とあらわすことができる。\(Fx\)は，台車が物体にした仕事\(W\)[J]であるので，速さ\(v\)[m/s]で運動している質量\(m\)[kg]の物体は，静止するまでに\(\displaystyle \frac{1}{2}mv^2\)の仕事をする能力をもっていることを意味している。よって，この物体のもつ運動エネルギー\(K\)[J]は，\(\displaystyle K=\frac{1}{2}mv^2\)とあらわすことができる。

運動エネルギーと仕事の関係

運動エネルギーと仕事の関係：\(W=\dfrac{1}{2}mv^2-\dfrac{1}{2}mv_0^2\)

物体に加えた仕事\(W\)[J]，質量\(m\)[kg]，変化後の速さ\(v\)[m/s]，変化前の速さ\(v_0\)[m/s]

今，質量\(m\)[kg]の物体が，速さ\(v_0\)[m/s]で運動している。この物体に，一定の大きさ\(F\)[N]の力を運動の向きに加えたところ，\(x\)[m]進んだときに速さが\(v\)[m/s]になったとする。この間の物体の運動方程式より，

\begin{eqnarray}a=\dfrac{F}{m}\end{eqnarray}

とあらわすことができる。これを，等加速度直線運動の公式に代入すると，
\begin{eqnarray}v^2-v_0^2&=&2\times \dfrac{F}{m}\times x\\ Fx&=&\dfrac{1}{2}mv^2-\dfrac{1}{2}mv_0^2\end{eqnarray}
となる。\(Fx\)は，台車に加えた仕事\(W\)[J]であるので，運動エネルギーと仕事の関係は，

\begin{eqnarray}W=\dfrac{1}{2}mv^2-\dfrac{1}{2}mv_0^2\end{eqnarray}

となる。これは，物体に加えた仕事と運動エネルギーの変化が等しいことを意味している。

重力による位置エネルギー

重力による位置エネルギ―：\(U=mgh\)

重力による位置エネルギー\(U\)[J]，質量\(m\)[kg]，重力加速度\(g\)[m/s²]，基準水平面からの高さ\(h\)[m]

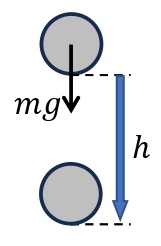
質量\(m\)[kg]の物体が，重力\(mg\)[N]を受けて\(h\)[m]降下するとする。このとき，重力は物体に対し\(mg\cdot h\)[J]の仕事をする。仕事と運動エネルギーの関係より，物体はこの仕事の分だけ運動エネルギーが増え，他の物体に仕事を行うことが可能になる。つまり，物体は\(mgh\)[J]のエネルギーを蓄えていた，と考えることができる。よって，基準水平面から高さ\(h\)[m]の位置にある，質量\(m\)[kg]の物体がもつ重力による位置エネルギ―\(U\)[J]は，\(U=mgh\)とあらわされる。

重力による位置エネルギーの基準水平面は，自由に設定してもよい。水平基準面よりも高い場所にある物体の位置エネルギーは正となり，水平基準面よりも低い場所にある物体の位置エネルギーは負となる。

弾性力による位置エネルギー

弾性力による位置エネルギ―：\(\displaystyle U=\frac{1}{2}kx^2\)

弾性力による位置エネルギー\(U\)[J]，ばね定数\(k\)[N/m]，ばねの伸び（または縮み）\(x\)[m]

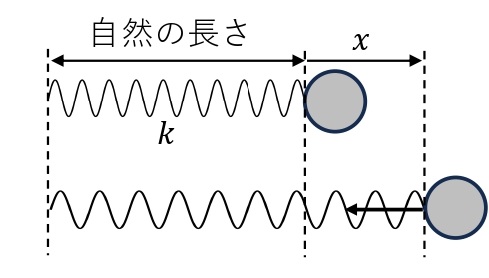
ばね（ばね定数\(k\)[N/m]）につけられた物体を自然長より\(x\)だけ伸ばし，手を離す。このとき，自然の長さにもどる間に物体は加速され，仕事をする能力を得る。つまり，物体はエネルギーを蓄えていた，と考えることができる。このようなエネルギーを弾性力による位置エネルギー，あるいは，単に弾性エネルギーという。

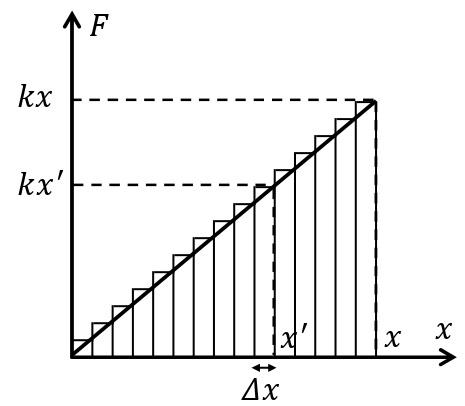
フックの法則より，ばねの伸びが\(x’\)[m]のとき，物体にはばねから\(F=kx’\)の弾性力をばねが縮む向きに受ける。この状態から微小距離\(\it\Delta x\)だけさらに縮んだとき，弾性力のする仕事は\(F\it\Delta x\)で近似できる（長方形の面積）。\(\it\Delta x\)をきわめて小さくとり，ばねの伸びが\(x\)から\(0\)になるまでの弾性力がする仕事\(W\)[J]を考えると，これは\(F\)-\(x\)グラフと\(x\)軸の間ではさまれた三角形の面積に等しくなり，

\begin{eqnarray}W=\dfrac{1}{2}\times x\times kx=\dfrac{1}{2}kx^2\end{eqnarray}

となる。\(x\)[m]縮められたばねが，自然の長さにもどるまでに物体にする仕事も同様に表される。よって，伸び(または縮み)が\(x\)[m]のばねにつけられた物体がもつ弾性力による位置エネルギー\(U\)[J]は\(\displaystyle U=\frac{1}{2}kx^2\)とあらわされる。

保存力

物体が移動するとき，物体にはたらく力のする仕事が途中の経路に関係なく始点と終点の位置だけで決まる場合，その力のことを保存力という。重力や弾性力，静電気力は保存力である。これに対し，動摩擦力や空気抵抗，人が加える力などは，その仕事が途中の経路によって変わるので，保存力ではない。

物体に保存力のみがはたらくとき，物体が点Aから基準点Oまで移動するときに保存力がする仕事$W$は移動経路によらず一定となる。この\(W\)を点Oを基準点とした点Aにおける物体の位置エネルギーという。

物体が点A（位置エネルギー\(U_A\)[J]）から点B（位置エネルギー\(U_B\)[J]）まで移動するとき，保存力のする仕事\(W_{AB}\)[J]は，\(W_{AB}=U_A-U_B\)であらわすことができる。

力学的エネルギー保存則

力学的エネルギー保存則

物体に仕事をする力が保存力のみである場合，
\begin{eqnarray}『力学的エネルギー』=一定\end{eqnarray}

運動エネルギーと位置エネルギーの和を力学的エネルギーという。

物体（質量\(m\)）に保存力だけが仕事をする場合，物体が点Aから点Bまで動く間に保存力のする仕事\(W_{AB}\)は，\(W_{AB}=U_A-U_B\)とあらわされる。点A，点Bでの物体の速さをそれぞれ\(v_A\)，\(v_B\)とすると，仕事と運動エネルギーの関係から，

\begin{eqnarray}W_{AB}&=&\dfrac{1}{2}mv_B^2-\dfrac{1}{2}mv_A^2\\ U_A-U_B&=&\dfrac{1}{2}mv_B^2-\dfrac{1}{2}mv_A^2\\ \dfrac{1}{2}mv_A^2+U_A&=&\dfrac{1}{2}mv_B^2+U_B&\end{eqnarray}

が成りたつ。つまり，物体に仕事をする力が保存力のみである場合，力学的エネルギーは一定に保たれる。

非保存力と力学的エネルギー

非保存力と力学的エネルギー

物体が非保存力によって仕事を受ける場合，『非保存力がする仕事』\(=\)『力学的エネルギーの変化』が成り立つ。

物体（質量\(m\)）に保存力の他，非保存力によっても仕事をする場合を考える。物体が点Aから点Bまで動く間に非保存力のする仕事を\(W\)，保存力のする仕事\(W_{AB}=U_A-U_B\)とする。点A，点Bでの物体の速さをそれぞれ\(v_A\)，\(v_B\)とすると，仕事と運動エネルギーの関係から，

\begin{eqnarray}W_{AB}+W&=&\dfrac{1}{2}mv_B^2-\dfrac{1}{2}mv_A^2\\ W&=&\left(\dfrac{1}{2}mv_B^2+U_B\right)-\left(\dfrac{1}{2}mv_A^2+U_A\right)\end{eqnarray}

が成りたつ。つまり，物体が非保存力によって仕事を受ける場合，『非保存力がする仕事』\(=\)『力学的エネルギーの変化』が成り立つ。