【高校物理の要点】平面上を伝わる波～波の波面、干渉、回折、反射、屈折・ホイヘンスの原理～

本記事では、『平面上を伝わる波～波の波面、干渉、回折、反射、屈折・ホイヘンスの原理～』について解説していきたいと思います。

平面上を伝わる波

波の波面

平面上を伝わる波において，振動の状態つまり位相が等しい点を連ねた面を波面という。波面が平面になる波を平面波，波面が球面になる波を球面波という。

波の干渉

波の干渉

　強めあう条件：\(\rm{\overline{S_1P}-\overline{S_2P}}=\it m\lambda\)　(\(m\)：整数)
　弱めあう条件：\(\displaystyle\rm{\overline{S_1P}-\overline{S_2P}}=\it \left(m\rm+\frac{1}{2}\right)\it\lambda\)　(\(m\)：整数)

波源\(\rm S_1\)と水面上の点Pとの距離\(\rm\overline{S_1P}\)[m]，波源\(\rm S_2\)と水面上の点Pとの距離\(\rm\overline{S_2P}\)[m]，波長\(\lambda\)[m]

波が重なって振動を強めあったり弱めあったりする現象を波の干渉という。水面上の2点\(\rm S_1\)，\(\rm S_2\)が同じ振動(同位相)をして，ともに波長\(\lambda\)の波が生じるときを考える。媒質中の点Pにおいて，\(\rm S_1P\)間の距離と\(\rm S_2P\)間の距離の差が\(m\lambda\)（\(m\)：整数）となるとき，\(\rm S_1\)から出た波と\(\rm S_2\)から出た波が\(\rm P\)において同位相で出会う。このとき，山と山，谷と谷で重なるので振動は強めあうことになる。このことから，

\begin{eqnarray}強めあう条件：\rm{\rm\overline{S_1P}-\rm\overline{S_2P}}=\it m\lambda　\rm(\it m\rm：整数)\end{eqnarray}

となる。

一方，媒質中の点\(\rm P\)において，\(\rm S_1P\)間の距離と\(\rm S_2P\)間の距離の差が\(\displaystyle\left(m+\dfrac{1}{2}\right)\lambda\)（\(m\)：整数）となるとき，\(\rm S_1\)から出た波と\(\rm S_2\)から出た波が\(\rm P\)において逆位相で出会う。このとき，山と谷で重なるので振動は弱めあうことになる。このことから，

\begin{eqnarray}弱めあう条件：\rm{\rm\overline{S_1P}-\rm\overline{S_2P}}=\it \left(m\rm+\dfrac{1}{2}\right)\it\lambda　\rm(\it m\rm：整数)\end{eqnarray}

となる。

\(\rm S_1\)，\(\rm S_2\)の振動が互いに逆のとき(逆位相)は，強め合う条件と弱め合う条件が入れ替わる。

波の回折

障害物に向かって波が進むとき，波が障害物の端から回り込み，障害物の裏側にまで広がる。これを波の回折という。

波の反射

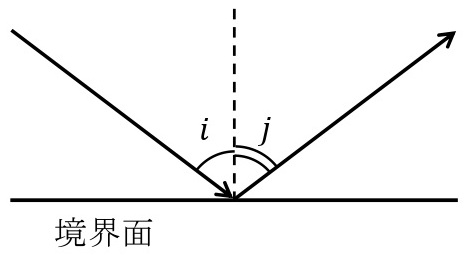
反射の法則：\(i=j\)

入射角\(i\)，反射角\(j\)

波が媒質の境界面に進んで反射するとき，境界面に垂直な直線と入射波の進行方向のなす角\(i\)を入射角，境界面に垂直な直線と反射波の進行方向のなす角\(j\)を反射角という。入射角\(i\)と反射角\(j\)の間に，反射の法則\(i=j\)が成りたつ。

波の屈折

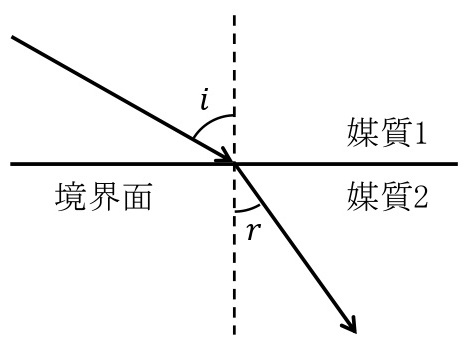
屈折の法則：\(\displaystyle\frac{\sin i}{\sin j}=\frac{v_1}{v_2}=\frac{\lambda_1}{\lambda_2}=n_{12}\)

入射角\(i\)，屈折角\(r\)，媒質1に対する媒質2の屈折率\(n_{12}\)
媒質1，媒質2での波の速さ\(v_1\)，\(v_2\)[m/s]，媒質1，媒質2での波の波長\(\lambda_1\)，\(\lambda_2\)[m]}

波がある媒質から異なる媒質に進むとき，波は屈折する。波が媒質の境界面に進んで屈折するとき，境界面に垂直な直線と入射波の進行方向のなす角\(i\)を入射角，境界面に垂直な直線と屈折波の進行方向のなす角\(r\)を屈折角という。このとき，以上の屈折の法則が成りたつ。

波の振動数\(f\)は屈折しても変化しないが，波の速さ\(v\)と波長\(\lambda\)は媒質が異なると変化する。\(n_{12}\)は2つの媒質によって決まる一定値であり，媒質1に対する媒質2の屈折率(相対屈折率)という。

ホイヘンスの原理

ホイヘンスは「ある時刻の波面において，波面上の各点が点波源となって，そこから出る素元波が無数に発生する。これらの素元波に共通する接する面が，次の瞬間の波面を形成する。」と考えた。これをホイヘンスの原理という。

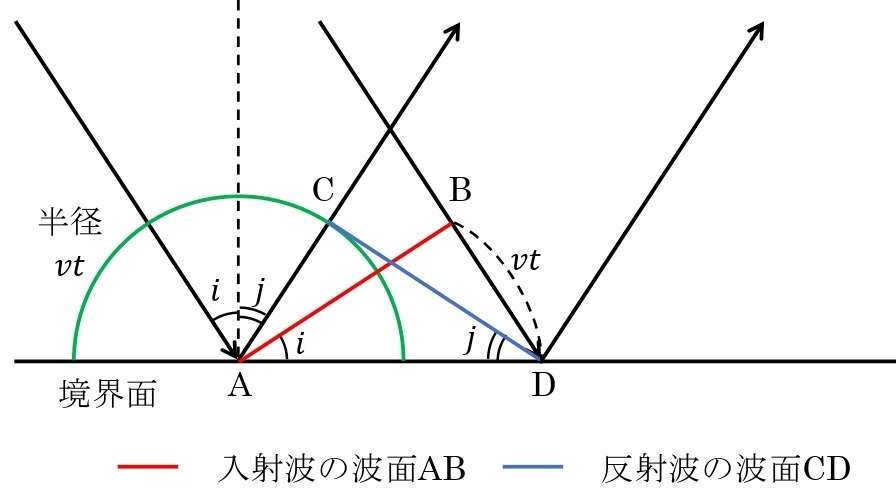
ホイヘンスの原理による反射の法則の説明

境界面に入射する波の波面がABに達した瞬間，Aからは反射の素源波が発生する。この瞬間からBが境界面上の点Dに達するまでの時間を\(t\)とする。波の速さを\(v\)とすると，\(t\)後の点Aを中心とする反射波の素元波は半径\(vt\)の半円形となる。点Dからこの半円に接線を引いて接点をCとすると，DCが反射波の波面になる。

直角三角形\(\Delta\rm ABD\)と\(\Delta\rm DCA\)について，\(\rm BD=CA=\it vt\)，ADは共通であるので，直角三角形\(\Delta\rm ABD\)と\(\Delta\rm DCA\)は合同となる。したがって，入射角\(i\)と反射角\(j\)は等しくなる。

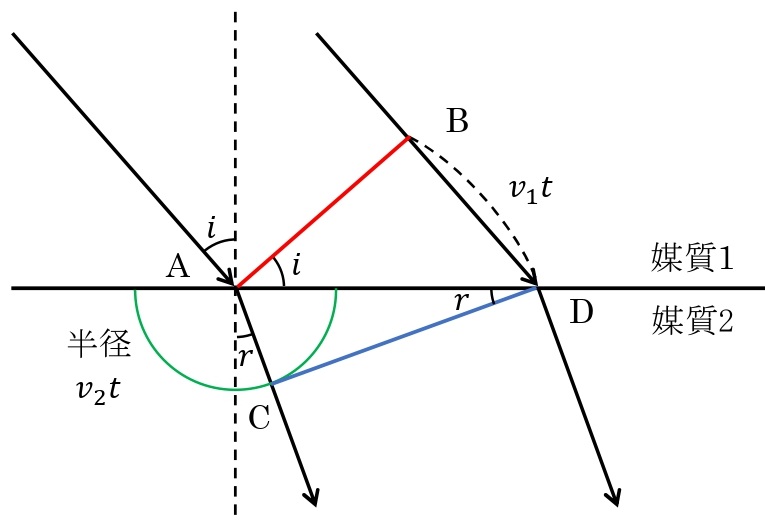
ホイヘンスの原理による屈折の法則の説明

境界面に入射する波の波面がABに達した瞬間，Aからは屈折の素源波が発生する。この瞬間からBが境界面上の点Dに達するまでの時間を\(t\)とする。媒質1の波の速度を\(v_1\)，媒質2の波の速度を\(v_2\)とすると，BDの長さは\(v_1t\)，点Aを中心とする屈折波の素元波は半径\(v_2t\)の半円形となる。点Dからこの半円に接線を引いて接点をCとすると，DCが屈折波の波面になる。

直角三角形\(\Delta\rm ABD\)と\(\Delta\rm DCA\)について，\(\angle\rm BAD=\it i\)，\(\angle\rm CDA=\it r\)，\(\rm BD=\it v_{\rm1}t\)，\(\rm AC=\it v_{\rm2}t\)であるので，\(\displaystyle\sin i=\frac{\rm BD}{\rm AD}=\frac{v_1t}{\rm AD}\)，\(\displaystyle\sin r=\frac{\rm AC}{\rm AD}=\frac{v_2t}{\rm AD}\)とあらわせる。よって，\(\displaystyle\frac{\sin i}{\sin r}=\frac{v_1}{v_2}\)となる。また，入射波の振動数を\(f\)とすると，媒質1と媒質2を進む波の振動数は屈折によって変化しないので，\(v_1=f\lambda_1\)，\(v_2=f\lambda_2\)となるので\(\displaystyle\frac{v_1}{v_2}=\frac{\lambda_1}{\lambda_2}\)となる。