【高校物理の要点】光の屈折とレンズ～光の反射と屈折・全反射・レンズ・球面鏡～

本記事では、『光の屈折とレンズ～光の反射と屈折・全反射・レンズ・球面鏡～』について解説していきたいと思います。

光

人間の目に感じる光を可視光線という。可視光の波長は，380nm～770nmであり，その色は波長(あるいは振動数)によって異なる。可視光の波長は長い方から短い方に並べると，

赤→橙→黄→緑→青→藍→紫

のようになる。太陽光のようにいろいろな波長の光を含む肉眼で白色に見える光を白色光という。一方，レーザー光等に見られるlつの波長からなる光を単色光という。

白色光をプリズムに入射させて白い紙に映すと，波長によって光の進路が変わり，赤から紫まで連続的に色が変わる帯（スペクトル）が見られる。これは，光の屈折率が波長によって異なる（波長が長いほど屈折率が小さい）ため，白色光に含まれる赤から紫の光が，それぞれの屈折率に応じて屈折するからである。このように，屈折によっていろいろな色の光に分かれることを光の分散という。

光がその波長よりも小さな粒子に当たると，通常の反射とは異なり，その粒子を中心とする球面波が生じ，四方に散る。これを光の散乱という。大気中の気体分子は，波長が短い青色の光ほど散乱されやすい。晴れた昼の空は青いのは，この散乱の性質によるためである。

光の速さ

光の速さは，真空中で\(c=2.99792458\times10^8\)m/sと定義されている。フィゾー(フランス)は，下のような実験により，初めて光の速さの測定を行った。

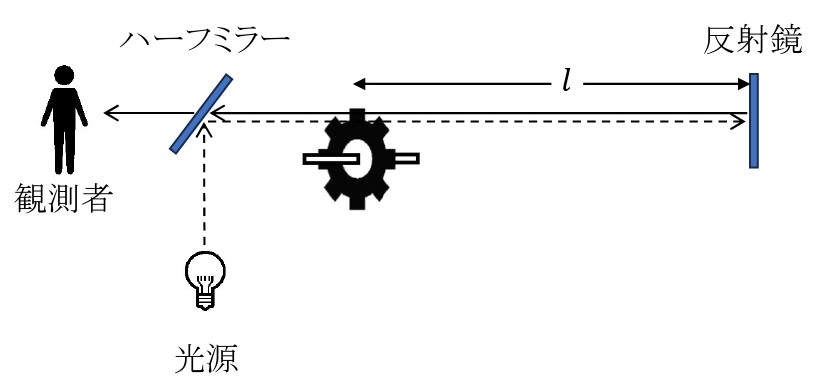
歯車から反射鏡までの距離を\(l\)[m]，光の速さを\(c\)[m/s]とする。上図で光が歯車を通過してから反射鏡で反射後再び歯車の位置に戻ってくるまでの時間は\(\displaystyle t=\frac{2l}{c}\)で表される。ここで歯車の歯数が\(N\)個，回転数(1秒当たりの回転の回数)\(n\)[回/s]とする。\(n\)を増やしていくと，光が往復してくる間に，歯車が歯1つ分だけ回転するとき，観測者には最初に光が届かなくなる。よって，\(\displaystyle t=\frac{1}{2Nn}\)と表される。以上から，

\begin{eqnarray}\displaystyle \frac{2l}{c}&=&\frac{1}{2Nn}\\ c&=&4Nnl\end{eqnarray}

と測定することができた。

光の反射・屈折

光は真空中や一様な媒質中では直進するが，異なる媒質との境界面では一部は反射し，一部は屈折する。

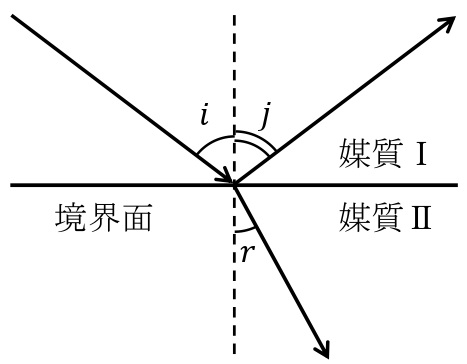
光の反射

入射角\(i\)と反射角\(j\)との間に反射の法則

\begin{eqnarray}i=j\end{eqnarray}

が成り立つ。

光の屈折

入射角を\(i\)，屈折角\(r\)，媒質Ⅰ中の光速を\(v_1\)，波長を\(\lambda_1\)，媒質Ⅱ中の光速を\(v_2\)，波長を\(\lambda_2\)とすると，屈折の法則

\begin{eqnarray}\displaystyle n_{12}=\frac{\sin i}{\sin r}=\frac{v_1}{v_2}=\frac{\lambda_1}{\lambda_2}\end{eqnarray}

が成り立つ。ここで，\(n_{12}\)は媒質Ⅰに対する媒質Ⅱの屈折率を表し，媒質Ⅰに対する媒質Ⅱの相対屈折率という。

一方，光が真空中からある媒質中へ入射するときの屈折率を，その媒質の絶対屈折率という。真空中の光速を\(c\)[m/s]，波長を\(\lambda_0\)[m]，媒質中の光速を\(v\)[m/s]，波長を\(\lambda\)[m]とすると\(\displaystyle n=\frac{c}{v}=\frac{\lambda_0}{\lambda}\)となる。媒質Ⅰ，媒質Ⅱの絶対屈折率を\(n_1\)，\(n_2\)とすると，媒質Ⅰに対する媒質Ⅱの相対屈折率\(n_{12}\)は，\(\displaystyle n_{12}=\frac{v_1}{v_2}=\frac{\frac{c}{v_1}}{\frac{c}{v_2}}=\frac{n_2}{n_1}\)と表すことができる。

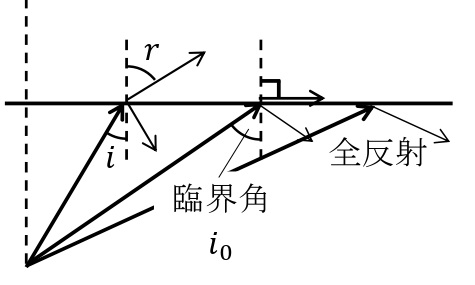
全反射

光が屈折率の大きい媒質から小さい媒質へ入射する場合は，入射角よりも屈折角のほうが大きい。このため，ある入射角\(i_0\)(\(i_0<90^\circ\))よりも入射角が大きくなると，屈折が起こらず全ての光が反射される。これを全反射という。また，この入射角\(i_0\)を臨界角という。臨界角では，屈折角が\(90^\circ\)となるので，屈折の法則から，

\begin{eqnarray}\displaystyle \frac{n_2}{n_1}&=&\frac{\sin90^\circ}{\sin i_0}\\ \sin i_0&=&\frac{n_1}{n_2}\end{eqnarray}

と表される。

レンズ

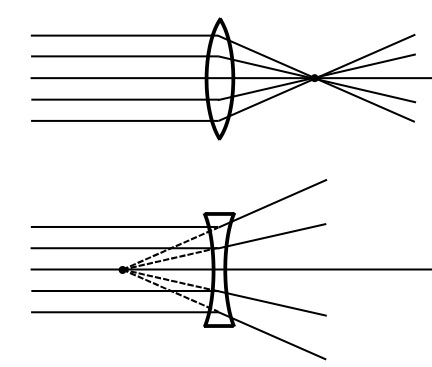
光の屈折を利用して光の進む方向を変え，光を集めたり広げたりできるようにした器具をレンズという。レンズには中心部が周辺部よりも厚い凸レンズと，中心部が周辺部より薄い凹レンズがある。

レンズの2つの球面の中心を結ぶ直線を光軸という。光軸に平行な光線が凸レンズを通過すると，光は光軸上の1点に光が集まる。また，光軸と平行な光線が凹レンズにを通過すると，レンズ前方の光軸上にある点から放射状に広がっているように進む。この点を焦点という。

凸レンズを通過する光の主な進路は以下の3つである。

• 光軸に平行にレンズに入射した光線は，屈折して焦点を通る。
• レンズの中心を通る光線は直進する。
• 焦点を通過後にレンズに入射した光線は，光軸に平行にすすむ。

凹レンズを通過する光の主な進路は以下の3つである。

• 光軸に平行にレンズに入射した光線は，焦点から出たかのように屈折して進む。
• レンズの中心を通る光線は直進する。
• 焦点に向かってレンズに入射した光線は，光軸に平行にすすむ。

レンズを通過した光が実際に集まってできる像を実像という。実際には光は集まっていないが，その位置から光が出ているかのように見える像を虚像という。凸レンズが作る像は，物体が焦点の外側にある場合は倒立実像，物体が焦点の内側にある場合は成立虚像ができる。凹レンズが作る像は，物体が焦点の内側外側にかかわらず，常に正立虚像ができる。

レンズの式

物体からレンズまでの距離を\(a\)[m]，レンズから像までの距離を\(b\)[m]，レンズの焦点距離（レンズから焦点までの距離）を\(f\)[m]の間には，次の公式が成り立つ。

\begin{eqnarray}\displaystyle&&レンズの公式：\frac{1}{a}+\frac{1}{b}=\frac{1}{f}\\&&倍率：m=\left|\frac{b}{a}\right|\end{eqnarray}

	凸レンズ		凹レンズ
\(f\)	\(f>0\)		\(f<0\)
\(a\)	\(a>0\)		\(a>0\)
\(b\)	実像：\(b>0\)	虚像：\(b<0\)	虚像：\(b<0\)

レンズの公式の導出

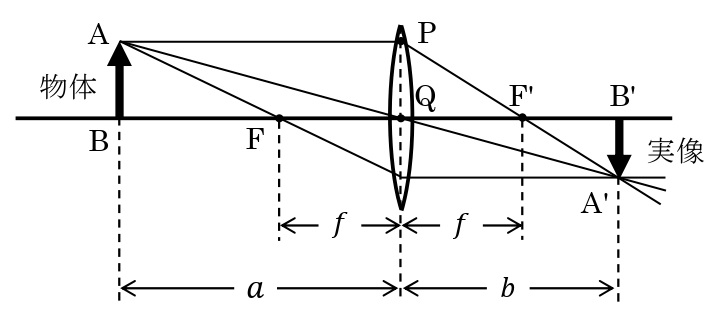
ここでは，凸レンズで実像が作られる場合について考える。物体からレンズまでの距離を\(a\)[m]，レンズから実像までの距離を\(b\)[m]，レンズの焦点距離を\(f\)[m]とする。

図より，\(\Delta\rm ABQ\)と\(\Delta\rm A’B’Q\)は相似の関係にあるので，倍率\(m\)は，

\begin{eqnarray}\displaystyle m=\frac{\rm A’B’}{\rm AB}=\frac{b}{a}　\cdots\cdots①\end{eqnarray}

とあらわせる。また，\(\Delta\rm POF’\)と\(\Delta\rm A’B’F’\)は相似の関係にあるので，倍率\(m\)は，

\begin{eqnarray}\displaystyle m=\frac{\rm A’B’}{\rm AB}=\frac{\rm A’B’}{\rm PQ}=\frac{b-f}{f}　\cdots\cdots②\end{eqnarray}

よって，①と②より，

\begin{eqnarray}\displaystyle m=\frac{\rm A’B’}{\rm AB}=\frac{b}{a}&=&\frac{b-f}{f}\\ \frac{1}{a}&=&\frac{1}{f}-\frac{1}{b}\\ \frac{1}{a}+\frac{1}{b}&=&\frac{1}{f} \end{eqnarray}

と変形できるので，レンズの公式が導出できた。凸レンズの虚像，凹レンズの虚像は，以上の凸レンズの実像の場合と同様，三角形の相似を利用すると，レンズの公式が得られる。

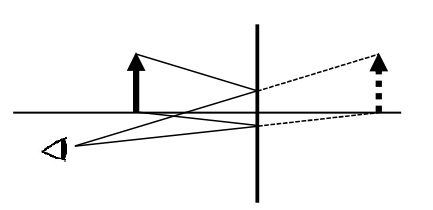
平面鏡

面が平面である鏡を平面鏡という。物体を平面鏡の前に置くと，反射面と対称な位置に像ができる。この像は，等倍(倍率1倍)の正立虚像である。

球面鏡

球面である鏡を球面鏡という。球面の内側を鏡面となっている鏡を凹面鏡，球面の外側が鏡面となっている鏡を凸面鏡という。球面鏡において，球の中心と鏡の中心をとを結ぶ直線を，光軸という。凹面鏡では，光軸なに平行な光は，反射後，光軸上の1点に光が集まる。また，凸面鏡では，光軸に平行な光は，反射後，鏡の後方の1点から出るように見える。この点を焦点という。

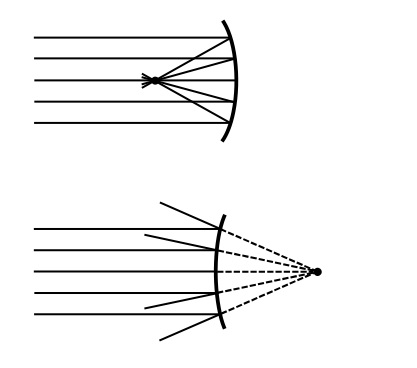
凹面鏡・凸面鏡

凹面鏡で反射した光の主な進路は以下の3つである。

• 光軸に平行に凹面鏡に入射した光線は，焦点に向かう向きに反射する。
• 凹面鏡の中心に向かって入射した光線は，光軸に関して対称に反射する。
• 焦点に向かって凹面鏡に入射した光線は，光軸に平行に反射する。

凸面鏡で反射した光の主な進路は以下の3つである。

• 光軸に平行に凸面鏡に入射した光線は，焦点から出たかのように反射する。
• 凸面鏡の中心に向かって入射した光線は，光軸に関して対称に反射する。
• 焦点に向かって凸面鏡に入射した光線は，光軸に平行に反射する。

球面鏡の式

物体から球面鏡までの距離を\(a\)[m]，球面鏡から像までの距離を\(b\)[m]，球面鏡の焦点距離（球面鏡から焦点までの距離）を\(f\)[m]の間には，次の公式が成り立つ。

\begin{eqnarray}\displaystyle&&球面鏡の式：\frac{1}{a}+\frac{1}{b}=\frac{1}{f}\\&&倍率：m=\left|\frac{b}{a}\right|\end{eqnarray}

	凹面鏡		凸面鏡
\(f\)	\(f>0\)		\(f<0\)
\(a\)	\(a>0\)		\(a>0\)
\(b\)	実像：\(b>0\)	虚像：\(b<0\)	虚像：\(b<0\)

球面鏡の式の導出

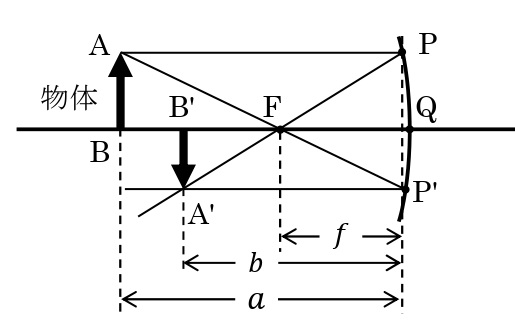
ここでは，凹面鏡で実像が作られる場合について考える。物体から凹面鏡までの距離を\(a\)[m]，凹面鏡から実像までの距離を\(b\)[m]，凹面鏡の焦点距離を\(f\)[m]とする。

図より，\(\Delta\rm ABF\)と\(\Delta\rm P’QF\)は相似の関係にあるので，倍率\(m\)は，

\begin{eqnarray}\displaystyle m=\frac{\rm P’Q}{\rm AB}=\frac{\rm QF}{\rm BF}=\frac{f}{a-f}　\cdots\cdots①\end{eqnarray}

とあらわせる。また，\(\Delta\rm FB’A’\)と\(\Delta\rm FQP\)は相似の関係にあるので，倍率\(m\)は，

\begin{eqnarray}\displaystyle m=\frac{\rm B’A’}{\rm QP}=\frac{\rm FB’}{\rm FQ}=\frac{b-f}{f}　\cdots\cdots②\end{eqnarray}

よって，①と②より，

\begin{eqnarray}\displaystyle m=\frac{\rm A’B’}{\rm AB}=\frac{f}{a-f}&=&\frac{b-f}{f}\\ bf+af&=&ab\\ \frac{1}{a}+\frac{1}{b}&=&\frac{1}{f} \end{eqnarray}

と変形できるので，球面鏡の式が導出できた。凸面鏡の場合は，以上の凹面鏡の場合と同様，三角形の相似を利用すると，凹面鏡の公式が得られる。