本記事では、『静磁場~電流のつくる磁場・電流が磁場から受ける力・ローレンツ力・ホール効果』について解説していきたいと思います。

予備校講師ともくん
専門科目:物理
経歴:東北大学物理学科
→東北大学大学院理学研究科物理学専攻
→公務員(教職ではない)
→塾業界に転職
→予備校&塾に出講中のプロ講師
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
磁気力
磁石の両端を磁極といい,磁極の強さを磁気量という。磁極にはN極とS極の2種類があり,地球上で磁針を観察したとき,北をさす磁極がN極,南をさす磁極がS極という。N極の磁気量を正,S極の磁気量を負にとる。磁石はN極のみ,S極のみといった片方の磁極のみからなる磁石はない。磁気量の単位にはウェーバ(記号Wb)を用いる。
磁気量の大きさが\(m_1\),\(m_2\)である2つの磁極が,磁極間の距離\(r\)で置かれているとき,2つの磁極の間にはたらく力の大きさ\(F\)は次の式で表される。
\begin{eqnarray}\displaystyle F=k_m\dfrac{m_1\cdot m_2}{r^2} \end{eqnarray}
これを磁気力に関するクーロンの法則という。磁極どうしにはたらく力は同種の極どうしは斥力,異種の極どうしは引力となる。\(k_m\)は比例定数であり,\(k_m=6.33\times10^4\)N・m²/Wb²である。
磁場
電場同様,磁荷に磁気力がはたらく空間を磁場(磁界)という。N極が磁気力を受ける向きを磁場の向き,磁極の磁気量1Wb当たりが受ける磁気力の大きさを磁場の強さと定める。電場と同じく,磁場は大きさと向きをもつベクトルである。磁場が\(\overrightarrow{H}\)の点に,\(m\)[Wb]の磁極を置くとき,磁極が受ける力\(\overrightarrow{F}\)[N]は次のように表される。
\begin{eqnarray}\displaystyle \overrightarrow{F}=m\overrightarrow{H}\end{eqnarray}
磁場の単位には,N/Wbを用いる。また,電場における電気力線同様,各点での磁場の状態は磁力線で表現できる。磁力線はN極から出てS極に入る。
電流のつくる磁場
直線電流の周囲の磁場:\(H=\displaystyle\frac{I}{2\pi r}\)
磁場の強さ\(H\)[A/m],電流\(I\)[A],電流からの距離\(r\)[m]
円形電流の中心の磁場:\(\displaystyle H=\frac{I}{2 r}\)
磁場の強さ\(H\)[A/m],電流\(I\)[A],円形電流の半径\(r\)[m]
ソレノイドの内部の磁場:\(H=nI\)
磁場の強さ\(H\)[A/m],電流\(I\)[A],単位長さ当たりの巻き数\(n\)[1/m]
直線電流がつくる磁場
十分に長い導線を流れる直線電流の周囲には導線に垂直な平面内で,同心円状の磁場が生じる。直線電流\(I\)[A]から\(r\)[m]離れた位置に生じる磁場の強さ\(H\)[N/Wb]は次の式で表される。
\begin{eqnarray}\displaystyle H=\frac{I}{2\pi r} \end{eqnarray}
磁場の向きは,右ねじの進む向きを電流の向きに合わせたときの右ねじの回る向きになる。これを右ねじの法則という。
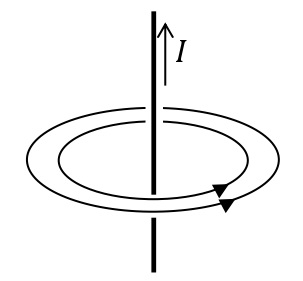
円形電流が作る磁場
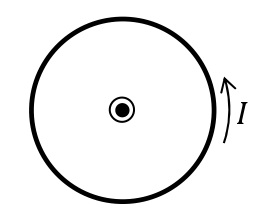
半径\(r\)[m]の円形導線に電流\(I\)[A]が図のように流れるとき,円の中心には磁場が紙面の裏から表へ向かう方向(右ねじを電流の向きに回したときの右ねじの進む向き)に生じる。その大きさ\(H\)[N/Wb]は次の式で表される。
\begin{eqnarray}\displaystyle H=\frac{I}{2 r} \end{eqnarray}
ソレノイドの電流がつくる磁場
導線を密に巻いた十分に長い円筒状コイルをソレノイドという。ソレノイドに電流を流すと,内部に磁場を生じる。この方向は円形電流の場合と同様,電流の方向に回したときの右ねじの進む向きである。ソレノイドの内部の磁場の強さ\(H\)[A/m]は,流れる電流を\(I\)[A],単位長さ当たりの巻数を\(n\)[1/m]とすると,次のように表される。
\begin{eqnarray}\displaystyle H=nI \end{eqnarray}
電流が磁場から受ける力
電流が磁場から受ける力
\(F=IBl\sin\theta\)
\(F=IBl\) (\(\theta=90^\circ\)のとき)
力の大きさ\(F\)[N],磁束密度の大きさ\(B\)[T],電流\(I\)[A],導線の長さ\(l\),磁場と電流がなす角度\(\theta\)
電流が磁場から受ける力
一様な磁場\(H\)[A/m]の中に磁場の方向と垂直に導線を置き,これに電流\(I\)[A]を流すと,この導線には磁場から力がはたらく。導線の長さ\(l\)[m]の部分が磁場から受ける力の大きさ\(F\)[N]は次の式で表される。
\begin{eqnarray}\displaystyle F=\mu IHl \end{eqnarray}
ここで,\(\mu\)は周囲の物質の種類によって定まる定数で,その物質の透磁率という。真空の透磁率は,\(\mu_0=1.26\times10^{-6}\)N/A²である。空気の透磁率はほぼ\(\mu_0\)に等しい。
直線電流が磁場から受ける力\(F\)[N]の向きは,電流\(I\)[A]の向きと磁場\(H\)[A/m]の向きのいずれにも垂直となる。この向きの関係は,開いた左手の3本の指(中指:電流,人差し指:磁場,親指:力)の関係に対応しており,これをフレミングの左手の法則という。
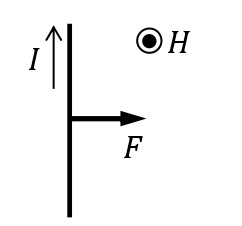
電流の向きと磁場の向きが角度\(\theta\)のときは,導線の長さ\(l\)[m]の部分が磁場から受ける力の大きさ\(F\)[N]は次の式で表される。
\begin{eqnarray}\displaystyle F=\mu IHl\sin\theta\end{eqnarray}
磁束密度
透磁率\(\mu\)の空間に磁場\(\overrightarrow{H}\)があるとき,\(\overrightarrow{B}=\mu\overrightarrow{H}\)を磁束密度という。単位はテスラ(記号T)を用いる。磁束密度\(B\)[T]の中に磁場の方向と垂直に導線を置き,これに電流\(I\)[A]を流す。このとき,導線の長さ\(l\)[m]の部分が磁場から受ける力の大きさ\(F\)[N]は次の式で表される。
\begin{eqnarray}\displaystyle F=IBl\end{eqnarray}
電流の向きと磁場の向きが角度\(\theta\)のときは,導線の長さ\(l\)[m]の部分が磁場から受ける力の大きさ\(F\)[N]は次の式で表される。
\begin{eqnarray}\displaystyle F=IBl\sin\theta \end{eqnarray}
平行電流が及ぼしあう力
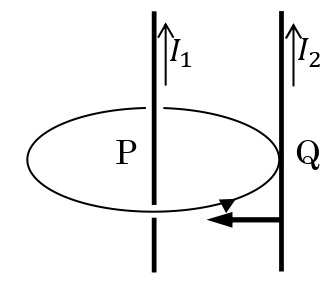
真空中に十分に長い2本の平行導線P,Qを\(r\)[m]離し,それぞれに電流\(I_1\),\(I_2\)[A]を流す。Pに流れる電流は導線Qの位置に大きさ\(H_1=\displaystyle\frac{I_1}{2\pi r}\)の磁場をつくる。この磁場によって,導線Qの長さ\(l\)[m]の部分は大きさ\(\displaystyle F=\mu_0I_2H_1l=\frac{\mu_0I_1I_2l}{2\pi r}\)の力を受ける。一方,導線Pが受ける力の大きさ\(F’\)[N]も同様に求めてみると,Qから同じ大きさの力を受けることがわかる。力の向きは電流の向きが同じときには引力,反対のときには斥力となる。
ローレンツ力
ローレンツ力:\(F=qvB\)
力の大きさ\(F\)[N],速さ\(v\)[m/s],磁束密度の大きさ\(B\)[T],電気量の大きさ\(q\)[C]
ローレンツ力
電気を帯びた粒子が磁場の中を運動すると力を受ける。この力をローレンツ力という。電気量\(q\)[C]をもつ粒子が磁束密度\(B\)[T]の磁場の中で,磁場に垂直な向きに速さ\(v\)[m/s]で運動しているとき,ローレンツ力の大きさ\(F\)[N]は次の式で表される。
\begin{eqnarray}\displaystyle F=qvB\end{eqnarray}
ローレンツ力の向きはフレミングの左手の法則で示される向き(速度ベクトルと垂直な方向)にはたらく。
一様な磁場内の荷電粒子の運動
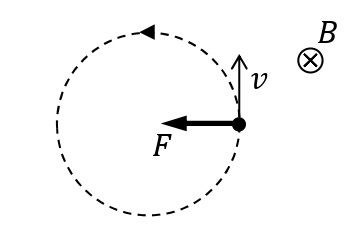
磁束密度\(B\)[T]の一様な磁場の中に,質量\(m\)[kg],電気量\(q\)[C]の粒子が,磁場に垂直に速さ\(v\)[m/s]で入射したとする。磁場からは粒子の運動方向に垂直にローレンツ力\(F=qvB\)[N]を受ける。このとき,ローレンツ力が向心力となって粒子は等速円運動をする。この円の半径\(r\)[m]とすると,
\begin{eqnarray}\displaystyle m\frac{v^2}{r}&=qvB\\ r&=\frac{mv}{qB}\end{eqnarray}
と表される。また,この等速円運動の周期\(T\)[s]は,\(\displaystyle T=\frac{2\pi r}{v}=\frac{2\pi m}{qB}\)と表される。この周期は粒子の速さ\(v\)にはよらない。つまり,同じ種類の粒子(例えば,電子)では,\(\displaystyle\frac{q}{m}\)の値が等しいので,同じ周期で円運動をする。これは,正体がわかっていない粒子の種類を特定する一つの手段となる。質量に対する電気量の比の値\(\displaystyle\frac{q}{m}\)[C/kg]を,その荷電粒子の比電荷という。
ホール効果
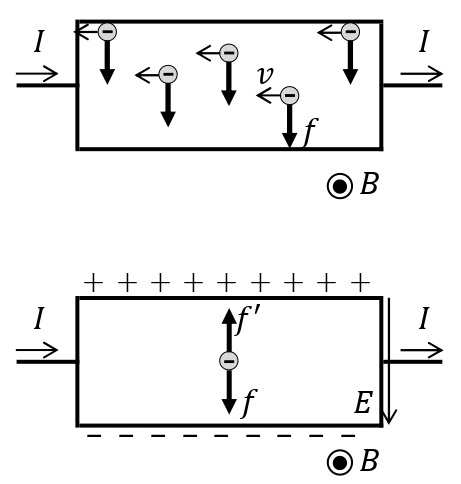
電流の流れる導体に磁場をかける。このとき,導体中のを流れる電子には,ローレンツ力がはたらく。これによって電荷の移動が起こり,導体の上面に正電荷,下面に負電荷が集まり,導体内に下向きの電場が生じる。この電場から受ける力\(f’\)とローレンツ力\(f\)がつり合うと,電子は直進するようになって,上面および下面の電荷は一定となり,導体上下面の間には電位差が生じる。この現象を,ホール効果といい,発生する電位差をホール電圧という。










コメント