【高校物理の要点】運動量の保存～力積と運動量変化・運動量保存則・反発係数～

本記事では、『運動量の保存～力積と運動量変化・運動量保存則・反発係数～』について解説していきたいと思います。

運動量と力積

運動量

運動量：\(\overrightarrow{p}=m\overrightarrow{v}\)

運動量\(\overrightarrow{p}\)[kg・m/s]，質量\(m\)[kg]，速度\(\overrightarrow{v}\)[m/s]

質量\(m\)の物体が速度\(\overrightarrow{v}\)で運動している。このとき，\(m\overrightarrow{v}\)をその物体の運動量という。これは，物体の運動の勢いをあらわす物理量である。

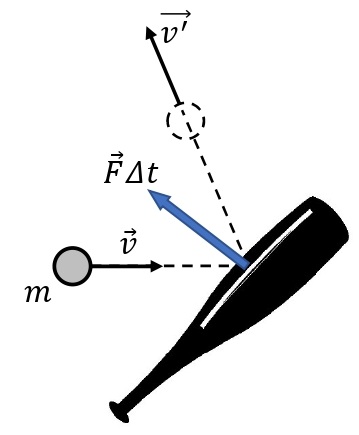
運動量と力積の関係

運動量と力積の関係：\(m\overrightarrow{v’}-m\overrightarrow{v}=\overrightarrow{F}\it\Delta t\)

質量\(m\)[kg]，変化前の速度\(\overrightarrow{v}\)[m/s]，変化後の速度\(\overrightarrow{v’}\)[m/s]，加えた力積\(\overrightarrow{F}\)[N]，時間\(\it\Delta t\)[s]

運動している質量\(m\)の物体に，力\(\overrightarrow{F}\)を加える。運動方程式より，

\begin{eqnarray}m\overrightarrow{a}=\overrightarrow{F}\end{eqnarray}

が成り立つ。また，力を加える前の速度を\(\overrightarrow{v_1}\)，力を加えた後の速度を\(\overrightarrow{v_2}\)，力を加えた時間を\(\it\Delta t\)とすると，

\begin{eqnarray}\overrightarrow{a}=\dfrac{\overrightarrow{v_2}-\overrightarrow{v_1}}{\it\Delta t}\end{eqnarray}

であらわされるので，

\begin{eqnarray}m\overrightarrow{a}&=&\overrightarrow{F}\\ m\dfrac{\overrightarrow{v_2}-\overrightarrow{v_1}}{\it\Delta t}&=&\overrightarrow{F}\\ m\overrightarrow{v_2}-m\overrightarrow{v_1}&=&\overrightarrow{F}\it\Delta t\end{eqnarray}

となる。この式は左辺が運動量の変化をあらわす。右辺は力\(\overrightarrow{F}\)と力を加えた時間\(\it\Delta t\)の積\(\overrightarrow{F}\it\Delta t\)のことを力積と呼ぶ。つまり，「物体の運動量の変化は加えられた力積に等しい」と言える。

運動量保存則

運動量保存則

外力がはたらかない（あるいは，はたらいていてもその力積が無視できる）とき，
\begin{eqnarray}運動量の和=一定\end{eqnarray}

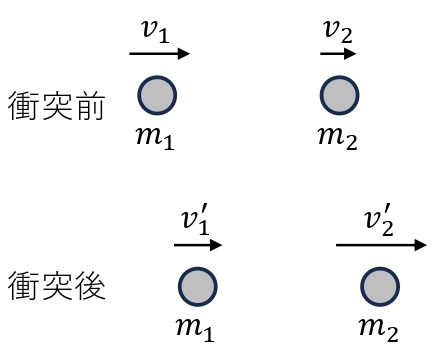
質量\(m_1\)の物体1が速度\(\overrightarrow{v_1}\)，質量\(m_2\)の物体2が速度\(\overrightarrow{v_2}\)で運動している。この2物体が衝突し，物体1が速度\(\overrightarrow{v’_1}\)，物体2が速度\(\overrightarrow{v’_2}\)となったとする。

物体1，物体2が衝突するときの接触時間を\(\it\Delta t\)，物体2が物体1から受ける力を\(\overrightarrow{F}\)とする。このとき，物体2の運動量の変化と力積の関係は，

\begin{eqnarray}m_2\overrightarrow{v’_2}-m_2\overrightarrow{v_2}=\overrightarrow{F}\it\Delta t\end{eqnarray}

とあらわされる。一方，作用反作用の法則より，物体1が物体2から受ける力は\(-\overrightarrow{F}\)となるので，物体1の運動量の変化と力積の関係は，

\begin{eqnarray}m_1\overrightarrow{v’_1}-m_1\overrightarrow{v_1}=-\overrightarrow{F}\it\Delta t\end{eqnarray}

とあらわされる。以上から\(\overrightarrow{F}\it\Delta t\)を消去すると，

\begin{eqnarray}m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}=m_1\overrightarrow{v’_1}+m_2\overrightarrow{v’_2}\end{eqnarray}

が得られる。つまり衝突前後において，物体1，物体2の運動量の和は保存していることがわかる。

複数個の物体に着目したとき，その物体間で及ぼしあっている力を内力という。これに対し，外部から力がはたらくとき，その力を外力という。作用反作用の法則より，2つの物体間の内力による力積は互いに逆向きで同じ大きさである。よって，内力による力積は，物体系全体としてみると互いに打ち消しあい，運動量の総和を変化させない。したがって，物体系が内力のみ(外力の和が0)のとき，全体の運動量の和は変化しない。これを運動量保存則という。

＜直線運動における運動量保存則の例＞

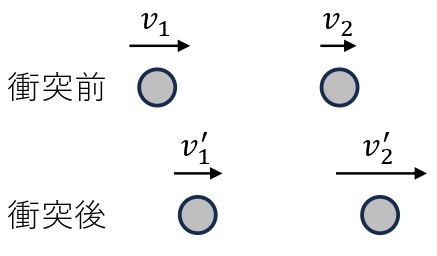
速度\(v_1\)[m/s]で直線上を運動する質量\(m_1\)の物体1が，同じ直線上を速度\(v_2\)[m/s]で運動する質量\(m_2\)の物体2に追いついて衝突し，速度がそれぞれ\(v’_1\)，\(v’_2\)[m /S]になったとする。衝突において，外力がはたらかないので，以下の運動量保存則が成り立つ。

\begin{eqnarray}m_1v_1+m_2v_2=m_1v’_1+m_2v’_2\end{eqnarray}

反発係数

反発係数

反発係数：\(\displaystyle e=-\frac{v_1′-v_2′}{v_1-v_2}\)

物体1と物体2の間の反発係数：\(e\)
衝突前の物体1の速度\(v_1\)[m/s]，衝突前の物体2の速度\(v_2\)[m/s]
衝突後の物体1の速度\(v_1’\)[m/s]，衝突後の物体2の速度\(v_2’\)[m/s]

2物体が同一直線上をともに運動している場合の衝突における反発係数を考える。同一直線上を運動する2つの物体1，物体2が衝突するとき，「衝突前の2物体近づく速さ」に対する「衝突前の2物体が遠ざかる速さ」の比の値\(e\)を，2物体の間の反発係数という。

数直線上を運動する物体1，物体2の衝突直前の速度をそれぞれ\(v_1\)，\(v_2\)，衝突直後の速度をそれぞれ\(v_1’\)，\(v_2’\)とすると，反発係数の式は，

\begin{eqnarray}e&=&\dfrac{衝突前の2物体が遠ざかる速さ}{衝突前の2物体近づく速さ}\\&=&\dfrac{|v’_1-v’_2|}{|v_1-v_2|}\\&=&-\dfrac{v’_1-v’_2}{v_1-v_2}\end{eqnarray}

となる。

壁や床等の動かないものとの衝突の場合，衝突に対して垂直な方向の衝突前後の速さを\(v\)，\(v’\)として，反発係数は

\begin{eqnarray}e=\dfrac{v’}{v}\end{eqnarray}

で与えられる。

反発係数\(e\)の値は衝突する2物体の組み合わせで決まる定数で，\(0≦e≦1\)の値をとる。\(e=1\)のときの衝突を弾性衝突といい，衝突前後で力学的エネルギーが保存される。\(0≦e<1\)のときの衝突を非弾性衝突といい，衝突前後で力学的エネルギーは減少する。\(e=0\)の場合を特に完全弾性衝突という。非弾性衝突で失われた力学的エネルギーは，熱の発生や物体の変形などに使われる。

床との斜めの衝突

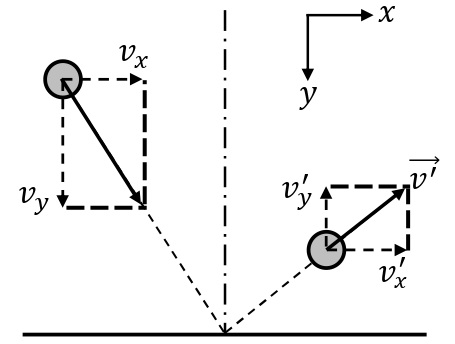
小球がなめらかな床に斜めに衝突する場合には，衝突の直前と直後の速度\(\overrightarrow{v}\)，\(\overrightarrow{v’}\)[m/s]を，床に対して平行な方向の成分\(v_x\)，\(v_x’\)[m/s]と，床に垂直な方向の成分\(v_y\)，\(v_y’\)[m/s]とに分解して扱う。床はなめらかなので，衝突の際に小球が受ける力積は衝突面に垂直な方向にはたらく。よって，衝突面に垂直な方向については，反発係数の式より，

\begin{eqnarray}e&=&-\dfrac{v_y’}{v_y}\\ v_y’&=&-ev_y\end{eqnarray}

となる。一方，衝突面に平行な方向には力積が加わらないので，

\begin{eqnarray}v_x’=v_x\end{eqnarray}

が成り立つ。