本記事では、『音~うなり・弦、気柱の振動・共振・ドップラー効果~』について解説していきたいと思います。

予備校講師ともくん
専門科目:物理
経歴:東北大学物理学科
→東北大学大学院理学研究科物理学専攻
→公務員(教職ではない)
→塾業界に転職
→予備校&塾に出講中のプロ講師
長い講師歴で数千人近くの生徒を送り出してきました。実際にいろいろな生徒と接する中で培った経験値を活かして、より多くの読者の皆様が将来の夢をかなえることができるようお手伝いできればと思っています。
音波
我々が聞く音は,空気の振動が縦波となって伝わったものである。これを音波という。音を特徴づける要素として,音の大きさ,音の高さ,音色の3つがあげられる。これを音の3要素という。
音の速さ
空気中を伝わる音の速さは,温度が高くなるほど大きくなる。\(t\)[\(^\circ\)C]の空気中の音の速さ\(V\)[m/s]は次のように表される。
\begin{eqnarray}V=331.5+0.6t\end{eqnarray}
音は空気のような気体だけではなく,液体や固体でも伝わる。一般的に,気体,液体,固体の順に音速は大きくなる。
うなり
振動数がわずかに異なる2つの音が同時に鳴ると音の大小が周期的にくり返されて聞こえる。このような現象をうなりという。振動数\(f_1\),\(f_2\)の音波が干渉するとき,単位時間当たり\(|f_1-f_2|\)回のうなりが観測される。
\begin{eqnarray}うなりの回数:f=|f_1-f_2|\end{eqnarray}
弦の振動
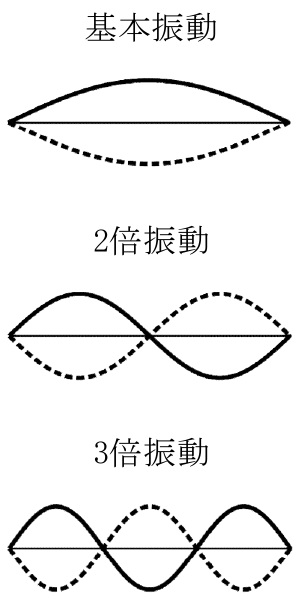
両端を固定した弦をはじくと,弦の両端が節となる定在波が発生する。このとき,その状態を弦の固有振動といい,そのときの振動数を固有振動数という。弦にできる腹の個数が\(m\)個の振動を\(m\)倍振動という。\(m=1\)の振動を特に基本振動という。
\(m\)倍振動の波長は,弦の長さを\(l\)[m]とすると,
\begin{eqnarray}弦の固有振動:\displaystyle\lambda_m=\frac{2l}{m} (m=1,2,3,\cdots)\end{eqnarray}
とあらわすことができる。また,弦を伝わる波の速さを\(v\)[m/s]とすると,固有振動数\(f_m\)[Hz]は,
\begin{eqnarray}\displaystyle f_m=\frac{v}{\lambda_m}=m\cdot\frac{v}{2l} (m=1,2,3,\cdots)\end{eqnarray}
となる。
気柱の振動
一端の閉じた管を閉管といい,両端の聞いた管を開管という。
開口端近くで空気が振動すると,特定の振動数に対して管内の気柱に固有振動が生じる。このとき,閉口端(管の底)では固定端反射が起こり定常波の節となり,管口である開口端では自由端反射が起こり定常波の腹となる。
閉管
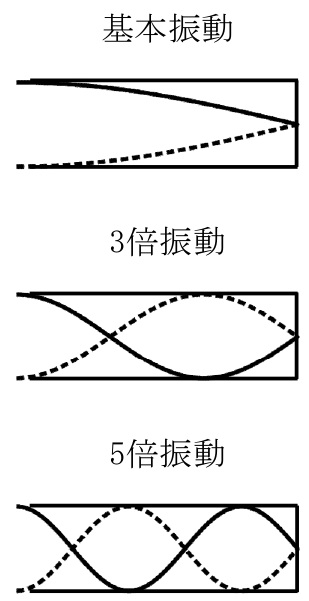
気柱の長さ\(l\)[m]の閉管では,音の速さを\(V\)[m/s]とすると,閉管の固有振動の波長\(\lambda_{2m-1}\)[m]と固有振動数\(f_{2m-1}\)[Hz]は次のようになる。
\begin{eqnarray}\displaystyle\lambda_{2m-1}&=&\frac{4l}{2m-1} (m=1,2,3,\cdots)\end{eqnarray}
\begin{eqnarray}\displaystyle f_{2m-1}&=&\frac{V}{\lambda_{2m-1}}\\ &=&(2m-1)\cdot\frac{V}{4l} (m=1,2,3,\cdots)\end{eqnarray}
\(m=1,2,3,\cdots\)のときの固有振動をそれぞれ基本振動,3倍振動,5倍振動\(\cdots\)と呼ぶ。
開管
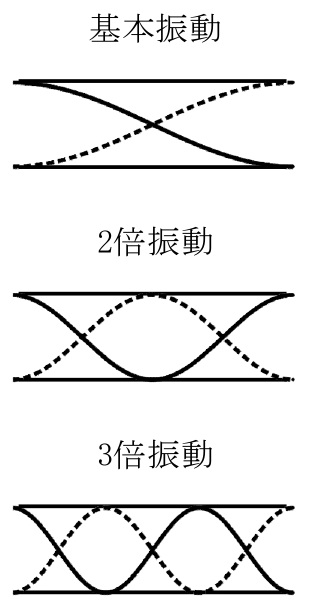
気柱の長さ\(l\)[m]の開管では,音の速さを\(V\)[m/s]とすると,固有振動の波長\(\lambda_m\)[m]と固有振動数\(f_m\)[Hz]は次のようになる。
\begin{eqnarray}\displaystyle\lambda_m&=&\frac{2l}{m} (m=1,2,3,\cdots)\end{eqnarray}
\begin{eqnarray}\displaystyle f_m&=&\frac{V}{\lambda_m}\\ &=&m\cdot\frac{V}{2l} (m=1,2,3,\cdots)\end{eqnarray}
\(m=1,2,3,\cdots\)のときの固有振動をそれぞれ基本振動,2倍振動,3倍振動\(\cdots\)と呼ぶ。
開口端補正
実際の開口端の腹の位置は,管口より少し外側に出ている。管口から腹の位置までの長さを開口端補正とよぶ。
共振
多くの物体は弦や気柱と同様に,その物体に特有の固有振動をもつ。物体に,固有振動数と等しい振動数の周期的な力を加え続けると,物体の振動の振幅はしだいに増大ていく。この現象を共振または共鳴という。
音のドップラー効果
ドップラー効果:\(f’=\displaystyle\frac{V-v_o}{V-v_s}f\)
観測者の受け取る音波の振動数\(f’\)[Hz],音波の振動数\(f\)[Hz],時間\(t\)[s],音の速さ\(V\)[m/s]},音源の速度\(v_s\)[m/s],観測者の速度\(v_o\)[m/s]
救急車のサイレンの音は,救急車が近づくときは音が高く聞こえ,救急車が遠ざかるときは音が低く聞こえる。音源や観測者が動くことで,もとの振動数(音の高さ)と異なった振動数が観測される現象をドップラー効果という。
音源が動くとき
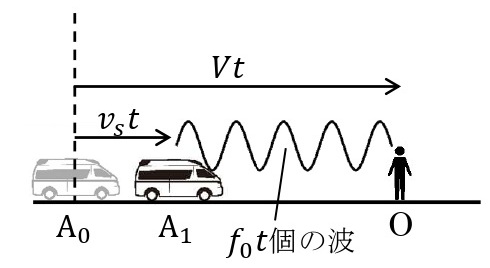
音源が動きながら音を出すと,動いている音源の進行方向の前方では波長が短くなって振動数が大きくなり,後方では波長が長くなって振動数が小さくなる。今,音源Sが振動数\(f_0\)[Hz]の音を出しながら,直線上を観測者Oに向かって速さ\(v_s\)[m/s]で進行する場合を考える。音源が位置A\(_0\)を通過したときに出した音波は,時刻\(t\)[s]に観測者に到達する。このとき,音速を\(V\)[m/s]とすると,A\(_0\)と観測者Oの距離は\(Vt\)[m]で表される。
一方,音源はこの時刻\(t\)[s]の間に\(v_st\)[m]だけ進み,位置A\(_1\)に到達する。この間に出した\(f_st\)個の波は,音源の前方A\(_1\)と観測者Oの間\((Vt-v_st)\)[m]にある。よって,音源の前方の音の波長\(\lambda’\)[m]は,
\begin{eqnarray}\displaystyle\lambda’=\frac{Vt-v_st}{f_0t}=\dfrac{V-v_s}{f_0}\end{eqnarray}
と表される。また,音源の前方に静止している観測者が聞く音の振動数を\(f’\)[Hz]とすると,
\begin{eqnarray}\displaystyle f’=\frac{V}{\lambda’}=\frac{V}{V-v_s}f_0\end{eqnarray}
となる。以上から,音源が観測者に近づくときは振動数が大きくなり,音が高く聞こえることがわかる。
観測者が動くとき
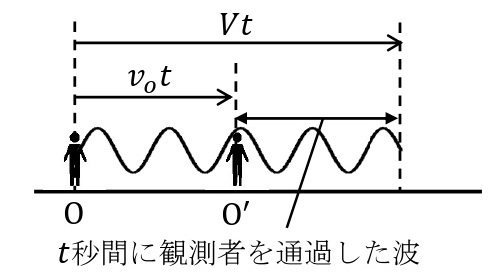
観測者が音源に近づくとき,観測される振動数は大きくなり,音が高く聞こえる。逆に,観測者が音源から遠ざかる場合は,音が低く聞こえる。今,振動数\(f_0\)[Hz]の音(音速\(V\)[m/s])を発する音源から観測者Oが速度\(v_o\)[m/s]で遠ざかる場合を考える。観測者Oを通過した音波は\(t\)[s]の間に\(Vt\)[m]進む。一方,この間に観測者Oは\(v_ot\)[m]進む。このとき,観測者を通過した音は\((Vt-v_ot)\)[m]の間にあり,その個数\(f’t\)は,\(\displaystyle f’t=\frac{Vt-v_ot}{\lambda}\)と表される。よって,\(\displaystyle\lambda=\frac{V}{f_0}\)より,
\begin{eqnarray}\displaystyle f’=\frac{V-v_o}{\lambda}=\frac{V-v_o}{V}f_0\end{eqnarray}
となる。
音源と観測者が動くとき
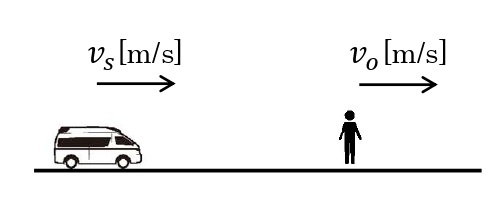
音源と観測者が同じ向きに動く場合を考える。音速を\(V\)[m/s],音源が発する音の振動数を\(f_0\)[Hz],音源から観測者に向かう向きを正として,音源の速度を\(v_s\)[m/s],観測者の速度を\(v_o\)とする。音源が動くので,音の波長\(\displaystyle\lambda’=\frac{V-v_s}{f_0}\)[m]の波が観測者に届くことになる。観測者が動くので,観測者が聞く音の振動数\(f’\)[Hz]は,
\begin{eqnarray}\displaystyle f’=\frac{V-v_o}{\lambda’}=\frac{V-v_o}{V-v_s}f_0\end{eqnarray}
となる。










コメント