【高校物理の要点】電流～オームの法則・抵抗の接続・キルヒホッフの法則・コンデンサーを含む直流回路～

本記事では、『電流～オームの法則・抵抗の接続・キルヒホッフの法則・コンデンサーを含む直流回路～』について解説していきたいと思います。

電流

荷電粒子の移動を電流という。導体中を流れる電流の向きと大きさは次のように定義される。

　電流の向き：正の電気が移動する向き

　電流の大きさ：単位時間当たりに導体の断面を通過する電気量の大きさ

電流の単位にはアンペア(記号A)を用いる。導体の断面を\(t\)[s]間に\(Q\)[C]の電気量が通過するときの電流\(I\)[A]は

\begin{eqnarray}\displaystyle I=\frac{Q}{t} \end{eqnarray}

と表される。

オームの法則

オームの法則

オームの法則：\(\displaystyle I=\frac{V}{R}\)

電流\(I\)[A]，電圧\(V\)[V]，抵抗\(R\)[Ω]

導体に流れる電流の大きさ\(I\)は導体に加える電圧\(V\)に比例する。これをオームの法則という。

\begin{eqnarray}\displaystyle I=\frac{V}{R} \end{eqnarray}

\(R\)は電流の流れにくさを表し，抵抗という。抵抗の単位はオーム（記号Ω）が用いられる。1Ωは，1Vの電圧を加えたとき，電流が1Aになるような抵抗を表す。

電圧降下

抵抗\(R\)[Ω]の導体に電流\(I\)[A]が流れると，抵抗の両端の間で\(RI\)[V]だけ電位が下がる。これを電圧降下という。

オームの法則の意味

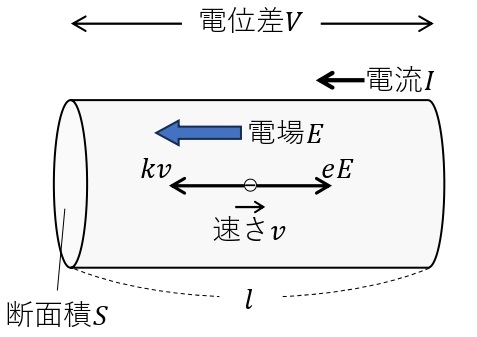
断面積\(S\)[m²]の一様な導体中に，自由電子（電気量\(-e\)[C]）が単位体積当たり\(n\)個存在しているとする。自由電子が速さ\(v\)[m/s]で移動するとき，時間\(t\)[s]の間にある断面を通過する電子の個数は\((vt\cdot S)\times n\)個になる。よって，時間\(t\)[s]の間にある断面を通過する電気量は\(Q=e\cdot (vt\cdot S)\times n\)であるので，流れる電流は\(\displaystyle I=\frac{Q}{t}=evSn\)で表される。

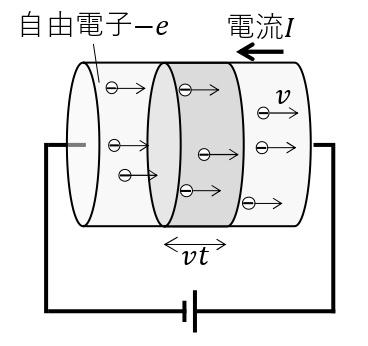
長さ\(l\)[m]，断面積\(S\)[m²]の導体の両端に電圧\(V\)[V]を加えると，導体内部には大きさ\(\displaystyle E=\frac{V}{l}\)[V/m]の電場が発生する。自由電子は電場から大きさ\(\displaystyle e\frac{V}{l}\)[N]の力を受けて動き始めるが，陽イオン等から抵抗力を受け，やがて一定の速さ\(v\)[m/s]で進むようになる。このとき，自由電子は陽イオンから速さ\(v\)に比例した抵抗力\(kv\)Nを受けているとすると，この抵抗力と電場から受ける力のつりあいより，

\begin{eqnarray}\displaystyle e\frac{V}{l}&=kv\\ v&=\frac{eV}{kl} \end{eqnarray}

が成り立つ。\(I=evSn\)の式に代入すると

\begin{eqnarray}\displaystyle I&=e\times\frac{eV}{kl}Sn\\ &=\frac{e^2nS}{kl}V \end{eqnarray}

これは，オームの法則を表している。ここで，\(\displaystyle R=\frac{kl}{e^2nS}\)とすると\(\displaystyle I=\frac{V}{R}\)が得られる。

抵抗率

抵抗率：\(\displaystyle R=\rho\frac{l}{S}\)

抵抗\(R\)[Ω]，抵抗率\(\rho\)[Ω・m]，抵抗の長さ\(l\)[m]，抵抗の断面積\(S\)[m²]

\(\displaystyle R=\frac{kl}{e^2nS}\)の式において，\(\displaystyle\frac{k}{e^2n}\)を\(\rho\)とすると抵抗\(R\)[Ω]は，

\begin{eqnarray}\displaystyle R=\rho\frac{l}{S} \end{eqnarray}

と表すことができる。比例定数\(\rho\)は，抵抗率と呼ばれ，物質に固有の値である。抵抗率の単位には，Ωメートル（記号Ω・m）が用いられる。

電気とエネルギー

ジュールの法則：\(\displaystyle Q=IVt=I^2Rt=\frac{V^2}{R}t\)

ジュール熱\(Q\)[J]，時間\(t\)[s]，電流\(I\)[A]，抵抗\(R\)[Ω]，電圧\(V\)[V]

電力：\(\displaystyle P=IV=I^2R=\frac{V^2}{R}\)

電力\(P\)[W]，電流\(I\)[A]，抵抗\(R\)[Ω]，電圧\(V\)[V]

導体に電流が流れると，熱が発生する。これは，電流のした仕事が熱に変わるためである。抵抗\(R\)[Ω]に電圧\(V\)[V]を加え，電流\(I\)[A]を\(t\)[s]の間流したとき，抵抗で発生する熱量\(Q\)[J]は，次の式に従うことがわかっている。

\begin{eqnarray}\displaystyle Q=IVt=I^2Rt=\frac{V^2}{R}t\end{eqnarray}

これをジュールの法則といい，発生する熱をジュール熱という。また，単位時間あたりのジュール熱\(\displaystyle P=\frac{Q}{t}\)を消費電力という。

\begin{eqnarray}\displaystyle P=IV=I^2R=\frac{V^2}{R} \end{eqnarray}

抵抗の接続

直列回路

合成抵抗

　直列接続：\(R=R_1+R_2\)

　並列接続：\(\displaystyle\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\)

合成抵抗\(R\)[Ω]，それぞれの抵抗\(R_1\)，\(R_2\)[Ω]

抵抗値が\(R_1\)，\(R_2\)[Ω]の抵抗を下図のように直列に接続し，起電力\(V\)[V]の電源を繋げる。このとき，2つの抵抗に流れる電流を\(I\)[A]とすると，各抵抗における電圧降下はそれぞれ\(V_1=R_1I\)，\(V_2=R_2I\)と表される。直列接続された抵抗の両端の電位差\(V\)は，\(V=V_1+V_2=(R_1+R_2)I\)と表されるので，この直列接続された合成抵抗は，\(R=R_1+R_2\)となる。

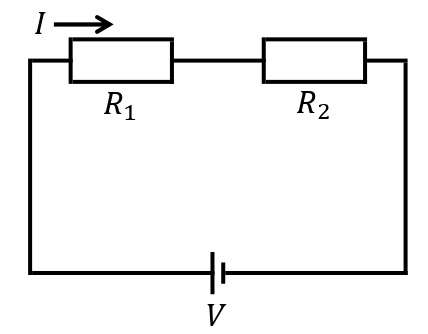
一般に，\(R_1，R_2，\cdots，R_n\)[Ω]の\(n\)個の抵抗を直列接続したときの合成抵抗\(R\)[Ω]は，次の式で与えられる。

\begin{eqnarray}R=R_1+R_2+\cdots+R_n \end{eqnarray}

並列回路

抵抗値が\(R_1\)，\(R_2\)[Ω]の抵抗を下図のように並列に接続し，起電力\(V\)[V]の電源を繋げる。このとき，各抵抗に加わる電圧は\(V\)[V]であるので，2つの抵抗に流れる電流をそれぞれ\(I_1\)[A]，\(I_2\)[A]とすると，\(\displaystyle I_1=\frac{V}{R_1}\)，\(\displaystyle I_2=\frac{V}{R_2}\)と表される。回路全体に流れる電流\(I\)[A]は，\(\displaystyle I=I_1+I_2=\frac{V}{R_1}+\frac{V}{R_2}=\left(\frac{1}{R_1}+\frac{1}{R_2}\right)V\)と表されるので，この直列接続された合成抵抗は，\(\displaystyle\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\)となる。

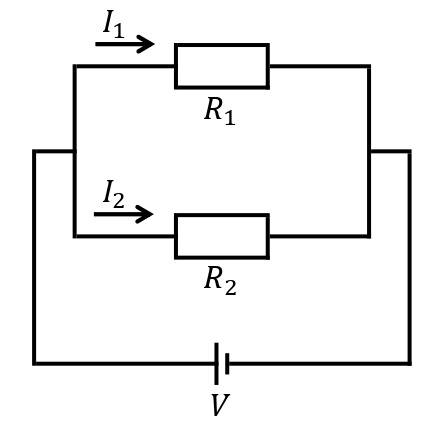
一般に，\(R_1，R_2，\cdots，R_n\)[Ω]の\(n\)個の抵抗を並列接続したときの合成抵抗\(R\)[Ω]は，次の式で与えられる。

\begin{eqnarray}\displaystyle\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\cdots+\frac{1}{R_n} \end{eqnarray}

電流計・電圧計

電流計

回路のある部分に流れる電流を測定する際，電流計を直列につないで用いる。電流計には，その内部に抵抗(内部抵抗)があるが，電流計をつなぐことによって回路を流れる電流が変化してしまう。この変化を少なくするため，電流計の内部抵抗は小さいほどよい。

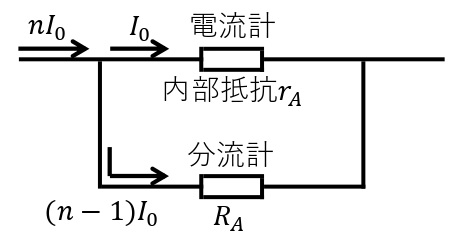
分流器

電流計の測定範囲をこえた大きな電流をはかるには，電流計と並列に抵抗を接続して電流計に流れる電流をの量を小さくすればよい。この抵抗を電流計の分流器という。電流計(内部抵抗\(r\))の測定範囲を\(n\)倍に広げる分流器の抵抗値\(R_A\)は次のようになる。

\begin{eqnarray}\displaystyle R_A=\frac{r_A}{n-1} \end{eqnarray}

電圧計

回路のある部分の電圧(電位差)を測定とする際，回路の2点に電圧計を並列につないで用いる。電圧計をつなぐことによって回路を流れる電流が変化してしまう。この変化を少なくするため，その内部抵抗は大きいほどよい。

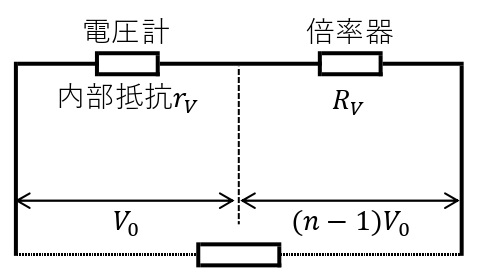
倍率器

電圧計の測定範囲をこえた大きな電圧をはかるには，電圧計に直列に抵抗を接続すればよい。この抵抗を電圧計の倍率器という。電圧計(内部抵抗\(r_V\))の測定範囲を\(n\)倍に広げる倍率器の抵抗値\(R_V\)は次のようになる。

\begin{eqnarray}\displaystyle R_V=(n-1)r_V\end{eqnarray}

電池の起電力と内部抵抗

電池の両端の電位差を端子電圧という。端子電圧\(V\)[V]を測定すると，\(V\)は電流\(I\)[A]が大きいほど小さくなる。これは，電池には内部抵抗\(r\)[Ω]を持ち，電流\(I\)が流れるときに電圧降下\(rI\)が起こるためである。

電池の端子電圧：\(V=E-rI\)

\(I=0\)のときの電池両端の電位差は\(E\)[V]となる。これを電池の起電力という。

キルヒホッフの法則

複雑な回路において，回路の各部分の電流や電圧は次の法則に従う。

キルヒホッフの法則

　第一法則：回路中の交点について
\begin{eqnarray}\displaystyle 『流れ込む電流の和』=『流れ出る電流の和』\end{eqnarray}

　第二法則：回路中一回りの閉じた経路について
\begin{eqnarray}\displaystyle 『起電力の和』=『電圧降下の和』\end{eqnarray}

＜キルヒホッフの法則の利用法＞

下図のような回路を考える。

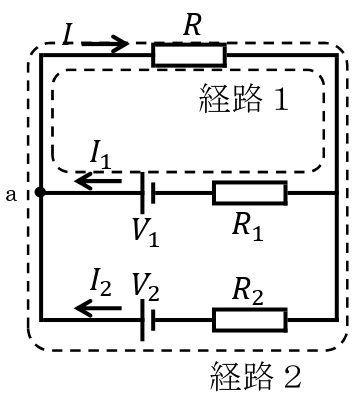
まず，回路中のa点にキルヒホッフの法則の第一法則を適用する。a点に流れ込む電流は\(I_1\)，\(I_2\)，流れ出る電流は\(I\)であるので，

\begin{eqnarray}\displaystyle I=I_1+I_2\hspace{3mm}\cdots\cdots\cdots\hspace{3mm}① \end{eqnarray}

が成り立つ。

次にキルヒホッフの第二法則を適用する。経路1の1周における電圧降下の和は\(RI+R_1I_1\)，起電力は\(V_1\)であるので，

\begin{eqnarray}\displaystyle V_1=IR+R_1I_1\hspace{3mm}\cdots\cdots\cdots\hspace{3mm}② \end{eqnarray}

が成り立つ。また，経路2の1周における電圧降下の和は\(RI+R_2I_2\)，起電力は\(V_2\)であるので，

\begin{eqnarray}\displaystyle V_2=IR+R_2I_2\hspace{3mm}\cdots\cdots\cdots\hspace{3mm}③\end{eqnarray}

が成り立つ。①～③の連立方程式を解くことで，\(I_1\)，\(I_2\)，\(I\)が求まる。

ホイートストンブリッジ

図のように4個の抵抗を組み合わせて，AB間に電圧をかける。 可変抵抗\(R_3\)[Ω]を変化させると，検流計Gを流れる電流が変化する。検流計Gに流れる電流が0Aになるように\(R_3\)[Ω]を調整する。

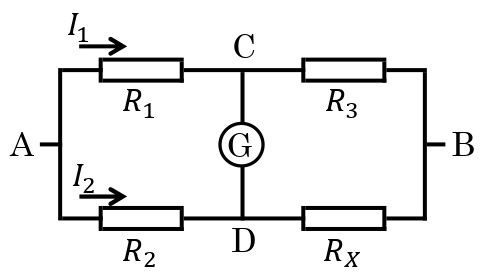
このとき，\(R_1\)[Ω]，\(R_3\)[Ω]の抵抗に流れる電流を\(I_1\)[A]，\(R_2\)[Ω]，\(R_X\)[Ω]に流れる電流を\(I_2\)[A]とすると，AC間とAD間の電圧降下，CB間とDB間の電圧降下はそれぞれ等しいので，\(R_1I_1=R_2I_2\)，\(R_3I_1=RI_2\)が成り立つ。以上から，

\begin{eqnarray}\displaystyle \dfrac{R_1}{R_2}=\dfrac{R_3}{R_X} \end{eqnarray}

が成り立つ。\(R_1\)，\(R_2\)の抵抗値がわかっており，可変抵抗\(R_3\)をこのように調節することによって，未知抵抗\(R_X\)を精密に測定することができる。 これをホイートストン・ブリッジという。

電位差計（ポテンショメーター）

図のような起電力が未知の電池の起電力(\(E_X\)[V]とする)を測定するための回路を電位差計という。太線は一様な抵抗線とする。まず，スイッチSが基準となる電池\(E_0\)[V]につなぐ。検流計Gに電流が流れない点P\(_0\)を探し，AP\(_0\)間の長さ\(l_0\)[m]を読み取る。次に，スイッチSを起電力が未知の電池\(E_X\)につなぐ。検流計Gに電流が流れない点P\(_X\)を探し，AP\(_X\)間の長さ\(l_X\)[m]を読み取る。

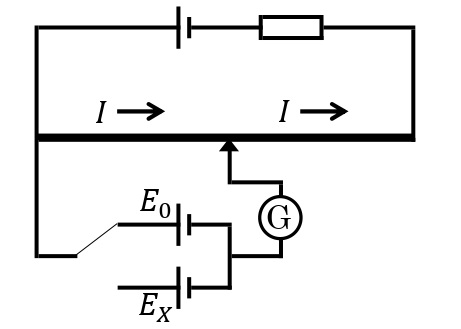
以上で得られた測定値には，\(\displaystyle\frac{E_X}{E_0}=\frac{l_X}{l_0}\)が成り立つので，未知の起電力\(E_X\)[V]を求めることができる。

コンデンサーを含む直流回路

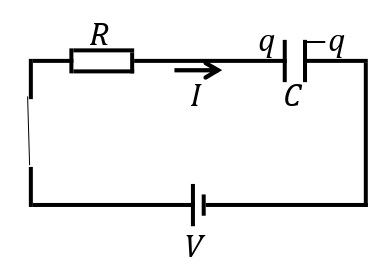
図のようなコンデンサーを含む回路について考える。 時間\(t=0\)sでスイッチを閉じる。スイッチを入れる前はコンデンサーには電荷は蓄えられていないものとする。キルヒホッフの法則より，

\begin{eqnarray}\displaystyle V=IR+\frac{q}{C}\hspace{3mm}\cdots\cdots\cdots\hspace{3mm}①\end{eqnarray}

が成り立つ。

(i)充電の開始時

スイッチを閉じた直後，コンデンサーに電荷が蓄えられていないので，\(q=0\)，よって，①式より，\(\displaystyle I=\frac{V}{R}\)となる。

(ii)充電の途中

蓄えられた電荷が\(q\)のとき，コンデンサーには電圧\(\displaystyle\frac{q}{C}\)がかかっているので，\(\displaystyle V-\frac{q}{C}=RI\)となり，コンデンサーに蓄えられている電荷が大きくなるにつれて，電流\(I\)は小さくなっていく。

(iii)十分時間が経過したとき

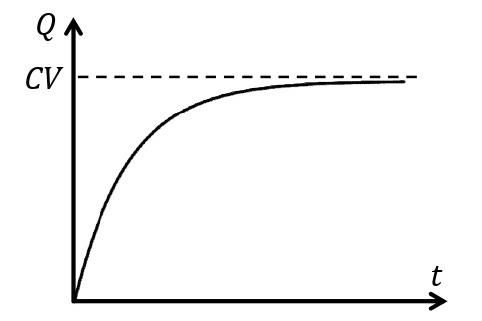
十分時間が経過すると，\(I=0\)となり，コンデンサーに蓄えられている電荷は\(q=CV\)で一定となる。

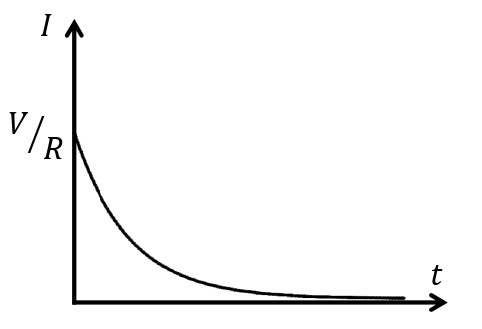
(i)～(iii)より，時間\(t\)の経過に伴う\(Q\)と\(I\)の変化は図のようになる。